Thm*  f:( f:( a bij a bij  a). InvFuns( a). InvFuns( a; a; a;f; a;f; y.least x: y.least x: . f(x)= . f(x)= y) y) | [nsub_bij_least_preimage_inverse] |
Thm* InvFuns(A;A;f;g)   ( ( i: i: . InvFuns(A;A;f{ . InvFuns(A;A;f{ i};g{ i};g{ i})) i})) | [compose_iter_inverses] |
Thm* InvFuns(   ;{xy:( ;{xy:(   )| )|  xy = <0,0> xy = <0,0>     };next_nat_pair;prev_nat_pair) };next_nat_pair;prev_nat_pair) | [next_nat_pair_vs_prev_nat_pair] |
Thm* InvFuns(A+B;i: 2 2 if i= if i= 0 0 A else B fi;union_to_sigma;sigma_to_union) A else B fi;union_to_sigma;sigma_to_union) | [union_sigma_inverses] |
Thm*  f:(A f:(A  B). Bij(A; B; f) B). Bij(A; B; f)   ( ( g:(B g:(B  A). InvFuns(A;B;f;g)) A). InvFuns(A;B;f;g)) | [bij_imp_exists_inv2] |
Thm*  f:(A f:(A  B). Bij(A; B; f) B). Bij(A; B; f)   ( ( g:(B g:(B  A). InvFuns(A;B;f;g)) A). InvFuns(A;B;f;g)) | [bij_imp_exists_inv_version2] |
Thm*  f:(A f:(A  B), g:(B B), g:(B  A). InvFuns(A;B;f;g) A). InvFuns(A;B;f;g)   Bij(A; B; f) Bij(A; B; f) | [fun_with_inv_is_bij_version2] |
Thm* InvFuns(A;B;f;g)   Bij(B; A; g) Bij(B; A; g) | [fun_with_inv2_is_bij_rev] |
Thm* InvFuns(A;B;f;g)   Bij(A; B; f) Bij(A; B; f) | [fun_with_inv2_is_bij] |
Thm* InvFuns(A;B;f;g)   InvFuns(A;B;f;h) InvFuns(A;B;f;h)   g = h g = h | [inv_funs_2_unique] |
Thm* InvFuns(A;B;f;g)   Surj(B; A; g) Surj(B; A; g) | [fun_with_inv2_is_surj_rev] |
Thm* InvFuns(A;B;f;g)   Inj(A; B; f) & Inj(B; A; g) Inj(A; B; f) & Inj(B; A; g) | [invfuns_are_inj] |
Thm* InvFuns(A;B;f;g)   Inj(B; A; g) Inj(B; A; g) | [fun_with_inv2_is_inj_rev] |
Thm* InvFuns(A;B;f;g)   Surj(A; B; f) & Surj(B; A; g) Surj(A; B; f) & Surj(B; A; g) | [invfuns_are_surj] |
Thm* InvFuns(A;B;f;g)   InvFuns(B;A;g;f) InvFuns(B;A;g;f) | [inv_funs_2_sym] |
Thm*  R:(A R:(A  B B  Prop). Prop).
Thm* (1-1-Corr x:A,y:B. R(x;y))
Thm*  
Thm* ( f:(A f:(A  B), g:(B B), g:(B  A). A).
Thm* (InvFuns(A;B;f;g) & ( x:A, y:B. R(x;y) x:A, y:B. R(x;y)   y = f(x) & x = g(y))) y = f(x) & x = g(y))) | [one_one_corr_rel_vs_invfuns] |
Thm* InvFuns(A; B; f; g)   InvFuns(A;B;f;g) InvFuns(A;B;f;g) | [inv_funs_iff_inv_funs_2] |
Thm*  f:(A f:(A  B), g:(B B), g:(B  A). SqStable(InvFuns(A;B;f;g)) A). SqStable(InvFuns(A;B;f;g)) | [sq_stable__inv_funs_2] |
Thm* InvFuns(A;B;f;g)   Surj(A; B; f) Surj(A; B; f) | [fun_with_inv2_is_surj] |
Thm* InvFuns(A;B;f;g)   Inj(A; B; f) Inj(A; B; f) | [fun_with_inv2_is_inj] |
| Thm* InvFuns(A;A;Id;Id) | [inv_funs_2_identity] |
Def A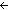  B == {fg:((A B == {fg:((A  B) B) (B (B  A))| fg/f,g. InvFuns(A;B;f;g) } A))| fg/f,g. InvFuns(A;B;f;g) } | [inv_pair] |
Def f is 1-1 corr ==  g:(B g:(B  A). InvFuns(A;B;f;g) A). InvFuns(A;B;f;g) | [is_one_one_corr] |
Def (x:A. B(x)) ~ (x':A'. B'(x'))
Def ==  f:(A f:(A  A'), g:(A' A'), g:(A'  A), F:(x:A A), F:(x:A  B(x) B(x)  B'(f(x))), G:(x:A B'(f(x))), G:(x:A  B'(f(x)) B'(f(x))  B(x)). B(x)).
Def == InvFuns(A;A';f;g) & ( u:A. InvFuns(B(u);B'(f(u));F(u);G(u))) u:A. InvFuns(B(u);B'(f(u));F(u);G(u))) | [one_one_corr_fams] |
Def A ~ B ==  f:(A f:(A  B), g:(B B), g:(B  A). InvFuns(A;B;f;g) A). InvFuns(A;B;f;g) | [one_one_corr_2] |