| 1 | 15. ( l:Alph*. l:Alph*. 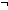 L(l @ x) = L(l @ y)) L(l @ x) = L(l @ y))   ( ( k: k: (n (n n), l:{l:(Alph*)| ||l|| = k n), l:{l:(Alph*)| ||l|| = k   }. }. 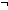 L(l @ x) = L(l @ y)) L(l @ x) = L(l @ y))
16. ( l:Alph*. l:Alph*. 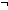 L(l @ x) = L(l @ y)) L(l @ x) = L(l @ y)) 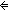  ( ( k: k: (n (n n), l:{l:(Alph*)| ||l|| = k n), l:{l:(Alph*)| ||l|| = k   }. }. 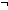 L(l @ x) = L(l @ y)) L(l @ x) = L(l @ y))
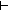 Fin( Fin( (n (n n)) n)) |
| 2 | 15. ( l:Alph*. l:Alph*. 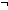 L(l @ x) = L(l @ y)) L(l @ x) = L(l @ y))   ( ( k: k: (n (n n), l:{l:(Alph*)| ||l|| = k n), l:{l:(Alph*)| ||l|| = k   }. }. 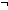 L(l @ x) = L(l @ y)) L(l @ x) = L(l @ y))
16. ( l:Alph*. l:Alph*. 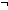 L(l @ x) = L(l @ y)) L(l @ x) = L(l @ y)) 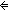  ( ( k: k: (n (n n), l:{l:(Alph*)| ||l|| = k n), l:{l:(Alph*)| ||l|| = k   }. }. 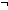 L(l @ x) = L(l @ y)) L(l @ x) = L(l @ y))
17. t:  (n (n n) n)
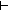 Dec(( Dec((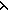 k. k. l:{l:(Alph*)| ||l|| = k l:{l:(Alph*)| ||l|| = k   }. }. 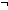 L(l @ x) = L(l @ y) L(l @ x) = L(l @ y)  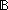 )(t)) )(t)) |
| 3 | 16. Dec( t: t: (n (n n). ( n). (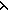 k. k. l:{l:(Alph*)| ||l|| = k l:{l:(Alph*)| ||l|| = k   }. }. 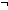 L(l @ x) = L(l @ y) L(l @ x) = L(l @ y)  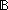 )(t)) )(t))
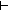 Dec( Dec( k: k: (n (n n), l:{l:(Alph*)| ||l|| = k n), l:{l:(Alph*)| ||l|| = k   }. }. 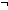 L(l @ x) = L(l @ y)) L(l @ x) = L(l @ y)) |