| 1 | 6.  x:Alph*. R(x,x) x:Alph*. R(x,x)
7.  x,y:Alph*. R(x,y) x,y:Alph*. R(x,y)   R(y,x) R(y,x)
8.  x,y,z:Alph*. R(x,y) & R(y,z) x,y,z:Alph*. R(x,y) & R(y,z)   R(x,z) R(x,z)
9.  x,y,z:Alph*. R(x,y) x,y,z:Alph*. R(x,y)   R((z @ x),z @ y) R((z @ x),z @ y)
10.  w:( w:( n n  Alph*). Alph*).  l:Alph*. l:Alph*.  i: i: n. R(l,w(i)) n. R(l,w(i))
11.  v:( v:( m m  Alph*). Alph*).  l:Alph*. L(l) l:Alph*. L(l) 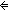  ( ( i: i: m. R(l,v(i))) m. R(l,v(i)))
12. Fin(Alph)
13. x: Alph*
14. y: Alph*
15. x@0: Alph*
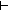 Dec(( Dec((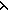 l.L(l @ x) = L(l @ y))(x@0)) l.L(l @ x) = L(l @ y))(x@0)) |
| 2 | 6.  x:Alph*. R(x,x) x:Alph*. R(x,x)
7.  x,y:Alph*. R(x,y) x,y:Alph*. R(x,y)   R(y,x) R(y,x)
8.  x,y,z:Alph*. R(x,y) & R(y,z) x,y,z:Alph*. R(x,y) & R(y,z)   R(x,z) R(x,z)
9.  x,y,z:Alph*. R(x,y) x,y,z:Alph*. R(x,y)   R((z @ x),z @ y) R((z @ x),z @ y)
10.  w:( w:( n n  Alph*). Alph*).  l:Alph*. l:Alph*.  i: i: n. R(l,w(i)) n. R(l,w(i))
11.  v:( v:( m m  Alph*). Alph*).  l:Alph*. L(l) l:Alph*. L(l) 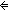  ( ( i: i: m. R(l,v(i))) m. R(l,v(i)))
12. Fin(Alph)
13. x: Alph*
14. y: Alph*
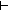 Dec( Dec( x@0:Alph*. x@0:Alph*. 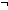 ( (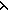 l.L(l @ x) = L(l @ y))(x@0)) l.L(l @ x) = L(l @ y))(x@0)) |
| 3 | 9. Dec( x@0:Alph*. ( x@0:Alph*. (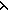 l.L(l @ x) = L(l @ y))(x@0)) l.L(l @ x) = L(l @ y))(x@0))
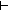 Dec( Dec( l:Alph*. L(l @ x) = L(l @ y)) l:Alph*. L(l @ x) = L(l @ y)) |