| 1 | 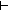 f f 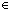  (n-1) (n-1)  {t:T| g(t) < n-1 } {t:T| g(t) < n-1 } |
| 2 | 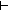 g g 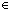 {t:T| g(t) < n-1 } {t:T| g(t) < n-1 }   (n-1) (n-1) |
| 3 | 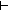 InvFuns( InvFuns( (n-1); {t:T| g(t) < n-1 }; f; g) (n-1); {t:T| g(t) < n-1 }; f; g) |
| 4 | 13. g@0: {t:T| g(t) < n-1 }   (n-1) (n-1)
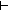 InvFuns( InvFuns( (n-1); {t:T| g(t) < n-1 }; f; g@0) (n-1); {t:T| g(t) < n-1 }; f; g@0) 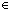 Prop Prop |
| 5 | 13. f1:  (n-1) (n-1)  {t:T| g(t) < n-1 } {t:T| g(t) < n-1 }
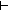 ( ( g@0:({t:T| g(t) < n-1 } g@0:({t:T| g(t) < n-1 }   (n-1)). InvFuns( (n-1)). InvFuns( (n-1); {t:T| g(t) < n-1 }; f1; g@0)) (n-1); {t:T| g(t) < n-1 }; f1; g@0)) 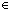 Prop Prop |