Thm* For any graph
 p:V List. 1 < ||p|| p:V List. 1 < ||p||   path(the_graph;p) path(the_graph;p)   path(the_graph;tl(p)) path(the_graph;tl(p)) | [path-tl] |
Thm*  k: k:  , L: , L: List. 0 < ||L|| List. 0 < ||L||   ( ( r: r:  . r- > L^k) . r- > L^k) | [Ramsey] |
Thm*  r,k: r,k: , L,R: , L,R: List. 2 List. 2 k k   ||R|| = ||L|| ||R|| = ||L||     ( ( i: i: ||L||. 0 < L[i] ||L||. 0 < L[i]   R[i]- > L[i--]^k) R[i]- > L[i--]^k)   r- > R^k-1 r- > R^k-1   r+1- > L^k r+1- > L^k | [Ramsey-recursion] |
Thm*  L: L: List, i,j: List, i,j: ||L||. 0 < L[i] ||L||. 0 < L[i]   L[i--][j] = if j= L[i--][j] = if j=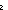 i i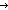 L[j]-1 else L[j] fi L[j]-1 else L[j] fi | [list-dec-select] |
Thm*  L: L: List, i: List, i: ||L||. 0 < L[i] ||L||. 0 < L[i]   ||L[i--]|| = ||L|| ||L[i--]|| = ||L||   | [list-dec-length] |
Thm*  L: L: List, i: List, i: ||L||. 0 < L[i] ||L||. 0 < L[i]   L[i--] L[i--]   List List | [list-dec_wf] |
Thm*  L: L: List. sum(L[i]-1 | i < ||L||)+1- > L^1 List. sum(L[i]-1 | i < ||L||)+1- > L^1 | [Ramsey-base-case] |
Thm*  k: k:  , L: , L: List. k-1- > L^k List. k-1- > L^k   ( ( i: i: ||L||. L[i] < k) ||L||. L[i] < k) | [trivial-arrows] |
Thm*  n,k: n,k: , c:( , c:( n n   k). k).  p:( p:( k k  ( ( List)). sum(||p(j)|| | j < k) = n & ( List)). sum(||p(j)|| | j < k) = n & ( j: j: k, x,y: k, x,y: ||p(j)||. x < y ||p(j)||. x < y   (p(j))[x] > (p(j))[y]) & ( (p(j))[x] > (p(j))[y]) & ( j: j: k, x: k, x: ||p(j)||. (p(j))[x] < n & c((p(j))[x]) = j) ||p(j)||. (p(j))[x] < n & c((p(j))[x]) = j) | [finite-partition] |
Def path(the_graph;p) == 0 < ||p|| & ( i: i: (||p||-1). p[i]-the_graph- > p[(i+1)]) (||p||-1). p[i]-the_graph- > p[(i+1)]) | [path] |
Def paren(T;s) == s = nil  (T+T) List (T+T) List 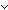 ( ( t:T, s':(T+T) List. s = ([inl(t)] @ s' @ [inr(t)]) & paren(T;s')) t:T, s':(T+T) List. s = ([inl(t)] @ s' @ [inr(t)]) & paren(T;s')) 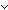 ( ( s',s'':(T+T) List. ||s'|| < ||s|| & ||s''|| < ||s|| & s = (s' @ s'') & paren(T;s') & paren(T;s'')) (recursive) s',s'':(T+T) List. ||s'|| < ||s|| & ||s''|| < ||s|| & s = (s' @ s'') & paren(T;s') & paren(T;s'')) (recursive) | [paren] |
Def L[i--] == mklist(||L||;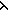 j.if j= j.if j=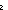 i i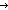 L[j]-1 else L[j] fi) L[j]-1 else L[j] fi) | [list-dec] |
Def r- > L^k ==  n: n: . r . r n n   ( ( G:({s:( G:({s:( n List)| ||s|| = k n List)| ||s|| = k   & ( & ( x,y: x,y: ||s||. x < y ||s||. x < y   s[x] < s[y]) } s[x] < s[y]) }   ||L||). ||L||).  c: c: ||L||, f:( ||L||, f:( L[c] L[c]   n). increasing(f;L[c]) & ( n). increasing(f;L[c]) & ( s: s: L[c] List. ||s|| = k L[c] List. ||s|| = k     ( ( x,y: x,y: ||s||. x < y ||s||. x < y   s[x] < s[y]) s[x] < s[y])   G(map(f;s)) = c)) G(map(f;s)) = c)) | [arrows] |