| | Some definitions of interest. |
|
| append | Def as @ bs == Case of as; nil 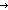 bs ; a.as' bs ; a.as' 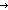 [a / (as' @ bs)] (recursive) [a / (as' @ bs)] (recursive) |
| | | Thm*  T:Type, as,bs:T List. (as @ bs) T:Type, as,bs:T List. (as @ bs) 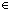 T List T List |
|
| list-connect | Def L-G- > *x == (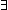 y y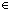 L.y-G- > *x) L.y-G- > *x) |
|
| connect | Def x-the_graph- > *y == 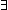 p:Vertices(the_graph) List. path(the_graph;p) & p[0] = x & last(p) = y p:Vertices(the_graph) List. path(the_graph;p) & p[0] = x & last(p) = y |
| | | Thm* For any graph
 x,y:V. x-the_graph- > *y x,y:V. x-the_graph- > *y 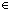 Prop Prop |
|
| gr_v | Def Vertices(t) == 1of(t) |
| | | Thm*  t:Graph. Vertices(t) t:Graph. Vertices(t) 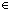 Type Type |
|
| graph | Def Graph == v:Type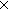 e:Type e:Type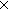 (e (e 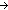 v v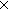 v) v)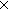 Top Top |
| | | Thm* Graph 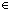 Type{i'} Type{i'} |
|
| iff | Def P 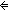 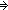 Q == (P Q == (P 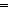 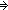 Q) & (P Q) & (P 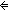 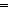 Q) Q) |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A 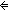 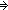 B) B) 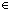 Prop Prop |
|
| l_exists | Def (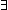 x x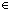 L.P(x)) == L.P(x)) == 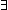 x:T. (x x:T. (x 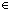 L) & P(x) L) & P(x) |
| | | Thm*  T:Type, L:T List, P:(T T:Type, L:T List, P:(T 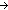 Prop). ( Prop). (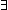 x x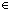 L.P(x)) L.P(x)) 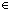 Prop Prop |
|
| l_member | Def (x 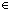 l) == l) == 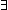 i: i: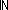 . i < ||l|| & x = l[i] . i < ||l|| & x = l[i] 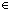 T T |
| | | Thm*  T:Type, x:T, l:T List. (x T:Type, x:T, l:T List. (x 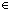 l) l) 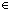 Prop Prop |