Nuprl - Proof: Ramsey-recursion 1 2 1 1 1 1

(99steps total) PrintForm Definitions Lemmas graph 1 2 Sections Graphs Doc

1. r:
2. k:
3. L: List
4. R: List
5. 2k
6. ||R|| = ||L||
7. i:||L||. 0 < L[i] R[i]- > L[i--]^k
8. r- > R^k-1
9. n:
10. r+1n
11. G: {s:(n List)| ||s|| = k & (x,y:||s||. x < y s[x] < s[y]) }||L||
12. c: ||R||
13. f: R[c](n-1)
14. increasing(f;R[c])
15. s:R[c] List. ||s|| = k-1 (x,y:||s||. x < y s[x] < s[y]) G(map(f;s) @ [(n-1)]) = c
16. 0 < L[c]
17. R[c]- > L[c--]^k
18. G:({s:(R[c] List)| ||s|| = k & (x,y:||s||. x < y s[x] < s[y]) }||L[c--]||). c@0:||L[c--]||, f:(L[c--][c@0]R[c]). increasing(f;L[c--][c@0]) & (s:L[c--][c@0] List. ||s|| = k (x,y:||s||. x < y s[x] < s[y]) G(map(f;s)) = c@0)
19. s: R[c] List
20. ||s|| = k
21. x,y:||s||. x < y s[x] < s[y]

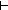G(map(f;s)) ||L||

By: Auto THEN Analyze THEN Try (Complete Auto) THEN RWO Thm* f:(AB), as:A List. ||map(f;as)|| = ||as|| 0 THEN RWO Thm* f:(AB), as:A List, n:||as||. map(f;as)[n] = f(as[n]) 0 THEN AllHyps (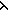h. ((FwdThru Thm* k:, f:(k). increasing(f;k) (x,y:k. x < y f(x) < f(y)) [h]) THEN (BackThru -1)) THEN EasyHyp)

Generated subgoals:

None

About:

(99steps total) PrintForm Definitions Lemmas graph 1 2 Sections Graphs Doc