| 1 | 20. f@0:  (L[c]-1) (L[c]-1)   R[c] R[c]
21. increasing(f@0;L[c]-1)
22.  s: s: (L[c]-1) List. ||s|| = k (L[c]-1) List. ||s|| = k     ( ( x,y: x,y: ||s||. x < y ||s||. x < y   s[x] < s[y]) s[x] < s[y])   G(map(f;map(f@0;s))) = c G(map(f;map(f@0;s))) = c
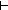 f o f@0[L[c]-1:=n-1] f o f@0[L[c]-1:=n-1]   L[c] L[c]   n n | 3 steps |
| |
| 2 | 20. f@0:  (L[c]-1) (L[c]-1)   R[c] R[c]
21. increasing(f@0;L[c]-1)
22.  s: s: (L[c]-1) List. ||s|| = k (L[c]-1) List. ||s|| = k     ( ( x,y: x,y: ||s||. x < y ||s||. x < y   s[x] < s[y]) s[x] < s[y])   G(map(f;map(f@0;s))) = c G(map(f;map(f@0;s))) = c
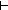 increasing(f o f@0[L[c]-1:=n-1];L[c]) & ( increasing(f o f@0[L[c]-1:=n-1];L[c]) & ( s: s: L[c] List. ||s|| = k L[c] List. ||s|| = k     ( ( x,y: x,y: ||s||. x < y ||s||. x < y   s[x] < s[y]) s[x] < s[y])   G(map(f o f@0[L[c]-1:=n-1];s)) = c) G(map(f o f@0[L[c]-1:=n-1];s)) = c) | 50 steps |
| |
| 3 | 20. f@0:  (L[c]-1) (L[c]-1)   R[c] R[c]
21. increasing(f@0;L[c]-1)
22.  s: s: (L[c]-1) List. ||s|| = k (L[c]-1) List. ||s|| = k     ( ( x,y: x,y: ||s||. x < y ||s||. x < y   s[x] < s[y]) s[x] < s[y])   G(map(f;map(f@0;s))) = c G(map(f;map(f@0;s))) = c
23. f1:  L[c] L[c]   n n
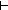 (increasing(f1;L[c]) & ( (increasing(f1;L[c]) & ( s: s: L[c] List. ||s|| = k L[c] List. ||s|| = k     ( ( x,y: x,y: ||s||. x < y ||s||. x < y   s[x] < s[y]) s[x] < s[y])   G(map(f1;s)) = c)) G(map(f1;s)) = c))  Prop Prop | 2 steps |