| | Some definitions of interest. |
|
| adjm_adj | Def t.adj == 2of(t) |
| | | Thm*  t:AdjMatrix. t.adj t:AdjMatrix. t.adj   t.size t.size   t.size t.size  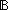 |
|
| adjm_size | Def t.size == 1of(t) |
| | | Thm*  t:AdjMatrix. t.size t:AdjMatrix. t.size   |
|
| adjmatrix | Def AdjMatrix == size:   size size   size size  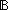 |
| | | Thm* AdjMatrix  Type Type |
|
| assert | Def 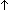 b == if b b == if b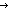 True else False fi True else False fi |
| | | Thm*  b: b: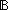 . b . b  Prop Prop |
|
| edge | Def x-the_graph- > y ==  e:Edges(the_graph). Incidence(the_graph)(e) = < x,y > e:Edges(the_graph). Incidence(the_graph)(e) = < x,y > |
| | | Thm* For any graph
 x,y:V. x-the_graph- > y x,y:V. x-the_graph- > y  Prop Prop |
|
| filter | Def filter(P;l) == reduce( a,v. if P(a) a,v. if P(a)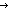 [a / v] else v fi;nil;l) [a / v] else v fi;nil;l) |
| | | Thm*  T:Type, P:(T T:Type, P:(T  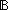 ), l:T List. filter(P;l) ), l:T List. filter(P;l)  T List T List |
|
| iff | Def P   Q == (P Q == (P   Q) & (P Q) & (P   Q) Q) |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A   B) B)  Prop Prop |
|
| int_seg | Def {i..j } == {k: } == {k: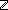 | i | i 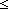 k < j } k < j } |
| | | Thm*  m,n: m,n: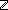 . {m..n . {m..n } }  Type Type |
|
| l_member | Def (x  l) == l) ==  i: i: . i < ||l|| & x = l[i] . i < ||l|| & x = l[i]  T T |
| | | Thm*  T:Type, x:T, l:T List. (x T:Type, x:T, l:T List. (x  l) l)  Prop Prop |
|
| mkgraph | Def < vertices = v, edges = e, incidence = f > == < v,e,f,o > |
| | | Thm*  v,e:Type, f:(e v,e:Type, f:(e  v v v), o:Top. < vertices = v, edges = e, incidence = f > v), o:Top. < vertices = v, edges = e, incidence = f >  Graph Graph |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 2of(p) B(a)). 2of(p)  B(1of(p)) B(1of(p)) |
|
| upto | Def upto(i;j) == if i < 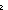 j j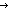 [i / upto(i+1;j)] else nil fi (recursive) [i / upto(i+1;j)] else nil fi (recursive) |
| | | Thm*  i,j: i,j: . upto(i;j) . upto(i;j)  {i..j {i..j } List } List |