| 2 | 22. L: Vertices(the_graph) List
23.  y:Vertices(the_graph). i-the_graph- > y y:Vertices(the_graph). i-the_graph- > y   (y (y  L) L)
24.  s':traversal(the_graph).
M(s' @ [inr(i) / s]) s':traversal(the_graph).
M(s' @ [inr(i) / s])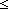 M([inr(i) / s])
& P(i,[inr(i) / s],s')
& list_accum(s',x'.dfs(the_obj;s';x');[inr(i) / s];L) = (s' @ [inr(i) / s]) M([inr(i) / s])
& P(i,[inr(i) / s],s')
& list_accum(s',x'.dfs(the_obj;s';x');[inr(i) / s];L) = (s' @ [inr(i) / s])
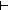  s':traversal(the_graph). M(s' @ s) s':traversal(the_graph). M(s' @ s)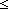 M(s) & P(i,s,s') & [inl(i) / list_accum(s',x'.( M(s) & P(i,s,s') & [inl(i) / list_accum(s',x'.( s',j. dfs(the_obj;s';j))(s',x');[inr(i) / s];L)] = (s' @ s) s',j. dfs(the_obj;s';j))(s',x');[inr(i) / s];L)] = (s' @ s)  traversal(the_graph) traversal(the_graph) | 2 steps |