| 2 | 9. df-traversal(the_graph;s)
10.  i:Vertices(the_graph). (inl(i) i:Vertices(the_graph). (inl(i)  s) s)   L1-the_graph- > *i L1-the_graph- > *i
11. ( i:Vertices(the_graph). L1-the_graph- > *i i:Vertices(the_graph). L1-the_graph- > *i    non-trivial-loop(the_graph;i)) non-trivial-loop(the_graph;i))
  (
( L1@0,L2:Vertices(the_graph) List.
L1 = (L1@0 @ L2) L1@0,L2:Vertices(the_graph) List.
L1 = (L1@0 @ L2)
  (
( s1,s2:traversal(the_graph).
s = (s2 @ s1) s1,s2:traversal(the_graph).
s = (s2 @ s1)  traversal(the_graph)
& paren(Vertices(the_graph);s1) & paren(Vertices(the_graph);s2)
& ( traversal(the_graph)
& paren(Vertices(the_graph);s1) & paren(Vertices(the_graph);s2)
& ( j:Vertices(the_graph).
((inl(j) j:Vertices(the_graph).
((inl(j)  s1) s1)   L1@0-the_graph- > *j)
& ((inl(j) L1@0-the_graph- > *j)
& ((inl(j)  s2) s2)   L2-the_graph- > *j & L2-the_graph- > *j &  L1@0-the_graph- > *j)))) L1@0-the_graph- > *j))))
12.  (inl(i) (inl(i)  s) s)
13. s2: traversal(the_graph)
14. l_disjoint(Vertices(the_graph)+Vertices(the_graph);s2;s)
15. paren(Vertices(the_graph);s2)
16. no_repeats(Vertices(the_graph)+Vertices(the_graph);s2)
17.  (inr(i) (inr(i)  s2) s2)
18.  j:Vertices(the_graph). (inr(j) j:Vertices(the_graph). (inr(j)  s2) s2)   i-the_graph- > *j i-the_graph- > *j
19. df-traversal(the_graph;([inl(i)] @ s2 @ [inr(i)]) @ s)
20.  i@0:Vertices(the_graph). L1 @ [i]-the_graph- > *i@0 i@0:Vertices(the_graph). L1 @ [i]-the_graph- > *i@0    non-trivial-loop(the_graph;i@0) non-trivial-loop(the_graph;i@0)
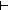  L1@0,L2:Vertices(the_graph) List. (L1 @ [i]) = (L1@0 @ L2) L1@0,L2:Vertices(the_graph) List. (L1 @ [i]) = (L1@0 @ L2)   ( ( s1,s2@0:traversal(the_graph). (([inl(i)] @ s2 @ [inr(i)]) @ s) = (s2@0 @ s1) s1,s2@0:traversal(the_graph). (([inl(i)] @ s2 @ [inr(i)]) @ s) = (s2@0 @ s1)  traversal(the_graph) & paren(Vertices(the_graph);s1) & paren(Vertices(the_graph);s2@0) & ( traversal(the_graph) & paren(Vertices(the_graph);s1) & paren(Vertices(the_graph);s2@0) & ( j:Vertices(the_graph). ((inl(j) j:Vertices(the_graph). ((inl(j)  s1) s1)   L1@0-the_graph- > *j) & ((inl(j) L1@0-the_graph- > *j) & ((inl(j)  s2@0) s2@0)   L2-the_graph- > *j & L2-the_graph- > *j &  L1@0-the_graph- > *j))) L1@0-the_graph- > *j))) | 135 steps |