| 1 | 7. L: Vertices(the_graph) List
8. no_repeats(Vertices(the_graph);L)
9.  y:Vertices(the_graph). (y y:Vertices(the_graph). (y  L) L)
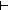 no_repeats(Vertices(the_graph);list_accum(s',x'.( no_repeats(Vertices(the_graph);list_accum(s',x'.( l,x. if P(x) l,x. if P(x)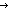 [x / l] else l fi)(s',x');nil;L)) & ( [x / l] else l fi)(s',x');nil;L)) & ( x:Vertices(the_graph). (x x:Vertices(the_graph). (x  list_accum(s',x'.( list_accum(s',x'.( l,x. if P(x) l,x. if P(x)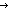 [x / l] else l fi)(s',x');nil;L)) [x / l] else l fi)(s',x');nil;L))   P(x)) P(x)) | 2 steps |