Thm*  x,n,m: x,n,m: . x . x n & x n & x m m   (nnsub(n;x) = nnsub(m;x) (nnsub(n;x) = nnsub(m;x) 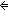  n = m) n = m) | [cancel_sub] |
Thm*  x,n,m: x,n,m: . n . n x & m x & m x x   (nnsub(x;n) = nnsub(x;m) (nnsub(x;n) = nnsub(x;m) 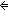  n = m) n = m) | [sub_cancel] |
Thm*  m,x: m,x: . m . m x x   ( ( n: n: . nnsub(x;m) . nnsub(x;m) n n 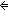  x x m+n) m+n) | [sub_less_eq_add] |
Thm*  n,m: n,m: . n . n m m   n<m+1 n<m+1 | [less_eq_imp_less_suc] |
Thm*  n,m: n,m: . n<m . n<m   ( ( x: x: . n<m+x) . n<m+x) | [less_imp_less_add] |
Thm*  b,c: b,c: . c . c b b   ( ( a: a: . nnsub(a;nnsub(b;c)) = nnsub(a+c;b)) . nnsub(a;nnsub(b;c)) = nnsub(a+c;b)) | [sub_sub] |
Thm*  a,b: a,b: . b . b a a   ( ( c: c: . nnsub(a;b)<c . nnsub(a;b)<c 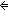  a<b+c) a<b+c) | [less_eq_sub_less] |
Thm*  c,b: c,b: . c . c b b   ( ( a: a: . nnsub(a+b;c) = a+nnsub(b;c)) . nnsub(a+b;c) = a+nnsub(b;c)) | [less_eq_add_sub] |
Thm*  n,m,i: n,m,i: . i<nnsub(n;m) . i<nnsub(n;m)   i+m<n i+m<n | [less_sub_add_less] |
Thm*  m,n: m,n: . n<m . n<m   n n nnsub(m;1) nnsub(m;1) | [sub_less_or] |
Thm*  n: n: . 0<n . 0<n   ( ( m: m: . pre(m) . pre(m) pre(n) pre(n) 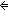  m m n) n) | [inv_pre_less_eq] |
Thm*  m: m: . 0<m . 0<m   ( ( n: n: . pre(m)<pre(n) . pre(m)<pre(n) 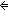  m<n) m<n) | [inv_pre_less] |
Thm*  n: n: . 0<n . 0<n   ( ( k: k: . nmod(nmod(k;n);n) = nmod(k;n)) . nmod(nmod(k;n);n) = nmod(k;n)) | [mod_mod] |
Thm*  n: n: . 0<n . 0<n   ( ( j,k: j,k: . nmod(nmod(j;n)+nmod(k;n);n) = nmod(j+k;n)) . nmod(nmod(j;n)+nmod(k;n);n) = nmod(j+k;n)) | [mod_plus] |
Thm*  n: n: . 0<n . 0<n   ( ( q,r: q,r: . nmod(q . nmod(q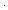 n+r;n) = nmod(r;n)) n+r;n) = nmod(r;n)) | [mod_times] |
Thm*  n,r: n,r: . r<n . r<n   ( ( q: q: . nmod(q . nmod(q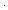 n+r;n) = r) n+r;n) = r) | [mod_mult] |
Thm*  n: n: . 0<n . 0<n   ndiv(0;n) = 0 ndiv(0;n) = 0 | [zero_div] |
Thm*  n: n: . 0<n . 0<n   nmod(0;n) = 0 nmod(0;n) = 0 | [zero_mod] |
Thm*  n: n: . 0<n . 0<n   ( ( k: k: . nmod(k . nmod(k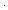 n;n) = 0) n;n) = 0) | [mod_eq_0] |
Thm*  n,k: n,k: . k<n . k<n   nmod(k;n) = k nmod(k;n) = k | [less_mod] |
Thm*  n,r: n,r: . r<n . r<n   ( ( q: q: . ndiv(q . ndiv(q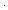 n+r;n) = q) n+r;n) = q) | [div_mult] |
Thm*  n,k,r: n,k,r: . ( . (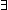 q: q: . k = q . k = q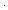 n+r n+r 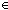  & r<n) & r<n)   nmod(k;n) = r nmod(k;n) = r | [mod_unique] |
Thm*  n,k,q: n,k,q: . ( . (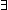 r: r: . k = q . k = q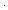 n+r n+r 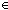  & r<n) & r<n)   ndiv(k;n) = q ndiv(k;n) = q | [ndiv_unique] |
Thm*  n: n: . 0<n . 0<n   ( ( k: k: . ndiv(k;n) . ndiv(k;n) k) k) | [div_less_eq] |
Thm*  k,n: k,n: . 0<n . 0<n   ( (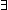 r,q: r,q: . k = q . k = q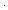 n+r n+r 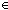  & r<n) & r<n) | [da] |
Thm*  P:( P:(  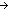 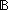 ). P(0) & ( ). P(0) & ( n: n: . ( . ( m: m: . m<n . m<n   P(m)) P(m))   P(n)) P(n))   ( ( n: n: . P(n)) . P(n)) | [gen_induction] |
Thm*  P:( P:(  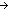 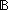 ). ( ). (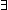 n: n: . P(n)) . P(n))   ( (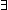 n: n: . P(n) & ( . P(n) & ( m: m: . m<n . m<n   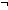 P(m))) P(m))) | [wop] |
Thm*  n,m: n,m: . n . n m & m m & m n n   n = m n = m | [less_equal_antisym] |
Thm*  m,n: m,n: . n<m . n<m   ( (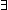 x: x: . m = n+x+1 . m = n+x+1 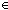  ) ) | [less_add_1] |
Thm*  m,n,x: m,n,x: . m . m n n   m m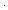 x x n n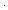 x x | [less_mono_mult] |
Thm*  m,n: m,n: . m<n . m<n   m m n n | [less_imp_less_or_eq] |
Thm*  m,n,x,q: m,n,x,q: . m . m x & n x & n q q   m+n m+n x+q x+q | [less_eq_less_eq_mono] |
Thm*  m,n,x: m,n,x: . m . m n & n n & n x x   m m x x | [less_eq_trans] |
Thm*  m,n,x: m,n,x: . m+x<n+x . m+x<n+x   m<n m<n | [less_mono_add_inv] |
Thm*  m,n,x: m,n,x: . m<n . m<n   m+x<n+x m+x<n+x | [less_mono_add] |
Thm*  m,n,x: m,n,x: . n . n x x   (m+n = x (m+n = x 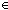  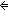  m = nnsub(x;n)) m = nnsub(x;n)) | [add_eq_sub] |
Thm*  m,n: m,n: . m<n . m<n   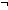 n<m+1 n<m+1 | [less_suc_not] |
Thm*  m,n: m,n: . 0<m & 0<n . 0<m & 0<n   (pre(m) = pre(n) (pre(m) = pre(n) 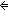  m = n) m = n) | [inv_pre_eq] |
Thm*  m,n: m,n: . 0<n . 0<n   (m = pre(n) (m = pre(n) 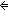  m+1 = n m+1 = n 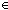  ) ) | [pre_suc_eq] |
Thm*  m,n: m,n: . n . n m m   nnsub(m;n)+n = m nnsub(m;n)+n = m 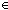  | [sub_add] |
Thm*  m,n: m,n: . . 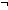 n = 0 n = 0 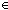    m<m+n m<m+n | [less_add_nonzero] |
Thm*  m,n: m,n: . m+n = m . m+n = m 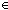    n = 0 n = 0 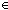  | [add_inv_0] |
Thm*  m,n: m,n: . . 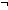 m<n & m<n & 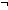 m = n m = n   n<m n<m | [less_cases_imp] |
Thm*  m,n: m,n: . m<n & . m<n & 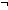 n = m+1 n = m+1 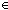    m+1<n m+1<n | [less_not_suc] |
Thm*  m,n: m,n: . m<n & . m<n & 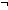 m+1 = n m+1 = n 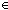    m+1<n m+1<n | [less_suc_eq_cor] |
Thm*  m,n: m,n: . m+1 . m+1 n n   m<n m<n | [or_less] |
Thm*  m,n: m,n: . m<n . m<n   m+1 m+1 n n | [less_or] |
Thm*  'a:S, f:('a 'a:S, f:('a 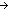 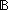 ), x1,x2:'a. f(x1) & ), x1,x2:'a. f(x1) & 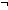 f(x2) f(x2)   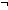 x1 = x2 x1 = x2 | [fun_eq_lemma] |
Thm*  m,n,x: m,n,x: . m<n & n<x . m<n & n<x   m<x m<x | [less_trans] |