| | Some definitions of interest. |
|
| assert | Def 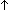 b == if b b == if b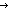 True else False fi True else False fi |
| | | Thm*  b: b: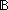 . b . b  Prop Prop |
|
| ncompose | Def ncompose(f;n;x) == if n=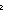 0 then x else f(ncompose(f;n-1;x)) fi (recursive) 0 then x else f(ncompose(f;n-1;x)) fi (recursive) |
| | | Thm*  'a:Type, n: 'a:Type, n: , x:'a, f:('a , x:'a, f:('a  'a). ncompose(f;n;x) 'a). ncompose(f;n;x)  'a 'a |
|
| eq_int | Def i=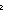 j == if i=j j == if i=j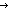 true true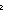 ; false ; false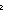 fi fi |
| | | Thm*  i,j: i,j: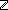 . (i= . (i=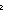 j) j)  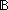 |
|
| not | Def 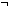 A == A A == A 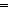 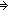 False False |
| | | Thm*  A:Prop. ( A:Prop. (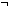 A) A)  Prop Prop |