| | Some definitions of interest. |
|
| his_num_rep | Def is_num_rep
Def ==  m: m: . .  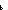 P: P:   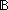
Def ==  m: m: . .   ((P(zero_rep)) ((P(zero_rep))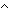 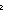 ( ( 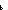 n: n: . (P(n)) . (P(n))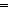 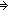 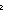 (P(suc_rep(n))))) (P(suc_rep(n)))))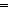 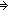 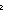 (P(m)) (P(m)) |
| | | Thm* is_num_rep  (hind (hind   hbool) hbool) |
|
| assert | Def 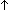 b == if b b == if b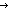 True else False fi True else False fi |
| | | Thm*  b: b: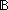 . b . b  Prop Prop |
|
| hrep_num | Def rep_num ==  n: n: . ncompose(suc_rep;n;zero_rep) . ncompose(suc_rep;n;zero_rep) |
| | | Thm* rep_num  (hnum (hnum   hind) hind) |
|
| label | Def t ...$L == t |
|
| nat | Def  == {i: == {i: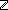 | 0 | 0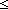 i } i } |
| | | Thm*   Type Type |
| | | Thm*   S S |