Thm*  'a:S. 'a:S.
Thm* all
Thm* ( e:'a. all e:'a. all
Thm* ( e:'a. ( e:'a. ( f:'a f:'a   hnum hnum   'a. exists_unique 'a. exists_unique
Thm* ( e:'a. ( e:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( fn1:hnum fn1:hnum   'a. and 'a. and
Thm* ( e:'a. ( e:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( fn1:hnum fn1:hnum   'a. (equal(fn1(0),e) 'a. (equal(fn1(0),e)
Thm* ( e:'a. ( e:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( fn1:hnum fn1:hnum   'a. ,all 'a. ,all
Thm* ( e:'a. ( e:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( fn1:hnum fn1:hnum   'a. ,( 'a. ,( n:hnum. equal n:hnum. equal
Thm* ( e:'a. ( e:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( fn1:hnum fn1:hnum   'a. ,( 'a. ,( n:hnum. (fn1(suc(n)) n:hnum. (fn1(suc(n))
Thm* ( e:'a. ( e:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( fn1:hnum fn1:hnum   'a. ,( 'a. ,( n:hnum. ,f n:hnum. ,f
Thm* ( e:'a. ( e:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( fn1:hnum fn1:hnum   'a. ,( 'a. ,( n:hnum. ,(fn1(n) n:hnum. ,(fn1(n)
Thm* ( e:'a. ( e:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( fn1:hnum fn1:hnum   'a. ,( 'a. ,( n:hnum. ,,n))))))) n:hnum. ,,n))))))) | [hnum_axiom] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( x:'a. all x:'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. and 'a. and
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. (equal(prim_rec(x,f,0),x) 'a. (equal(prim_rec(x,f,0),x)
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,all 'a. ,all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. equal m:hnum. equal
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. (prim_rec(x,f,suc(m)) m:hnum. (prim_rec(x,f,suc(m))
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ,f(prim_rec(x,f,m),m)))))) m:hnum. ,f(prim_rec(x,f,m),m)))))) | [hprim_rec_thm] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( x:'a. all x:'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. and 'a. and
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. (all( 'a. (all( n:hnum. equal(prim_rec_fun(x,f,0,n),x)) n:hnum. equal(prim_rec_fun(x,f,0,n),x))
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,all 'a. ,all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. all m:hnum. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. equal n:hnum. equal
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. (prim_rec_fun n:hnum. (prim_rec_fun
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. ((x n:hnum. ((x
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. (,f n:hnum. (,f
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. (,suc(m) n:hnum. (,suc(m)
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. (,n) n:hnum. (,n)
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. ,f n:hnum. ,f
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. ,(prim_rec_fun n:hnum. ,(prim_rec_fun
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. ,((x n:hnum. ,((x
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. ,(,f n:hnum. ,(,f
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. ,(,m n:hnum. ,(,m
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. ,(,pre(n)) n:hnum. ,(,pre(n))
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,( 'a. ,( m:hnum. ( m:hnum. ( n:hnum. ,,n))))))) n:hnum. ,,n))))))) | [hprim_rec_eqn] |
Thm* and(equal(pre(0),0),all( m:hnum. equal(pre(suc(m)),m))) m:hnum. equal(pre(suc(m)),m))) | [hpre_suc] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( x:'a. all x:'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. and 'a. and
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. (equal(simp_rec(x,f,0),x) 'a. (equal(simp_rec(x,f,0),x)
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ,all 'a. ,all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ,( 'a. ,( m:hnum. equal m:hnum. equal
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ,( 'a. ,( m:hnum. (simp_rec(x,f,suc(m)) m:hnum. (simp_rec(x,f,suc(m))
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ,( 'a. ,( m:hnum. ,f(simp_rec(x,f,m))))))) m:hnum. ,f(simp_rec(x,f,m))))))) | [hsimp_rec_thm] |
Thm* all( m:hnum. and(lt(m,suc(m)),lt(m,suc(suc(m))))) m:hnum. and(lt(m,suc(m)),lt(m,suc(suc(m))))) | [hless_suc_suc] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( x:'a. all x:'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. all 'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. exists n:hnum. exists
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ( n:hnum. ( fun:hnum fun:hnum   'a. simp_rec_rel 'a. simp_rec_rel
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ( n:hnum. ( fun:hnum fun:hnum   'a. (fun 'a. (fun
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ( n:hnum. ( fun:hnum fun:hnum   'a. ,x 'a. ,x
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ( n:hnum. ( fun:hnum fun:hnum   'a. ,f 'a. ,f
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ( n:hnum. ( fun:hnum fun:hnum   'a. ,n))))) 'a. ,n))))) | [hsimp_rec_exists] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( n:hnum. all n:hnum. all
Thm* ( n:hnum. ( n:hnum. ( f:'a f:'a
Thm* ( n:hnum. ( n:hnum. (  'a. all 'a. all
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. equal x:'a. equal
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. (exists( x:'a. (exists( fun:hnum fun:hnum   'a. simp_rec_rel(fun,x,f,n)) 'a. simp_rec_rel(fun,x,f,n))
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. ,and x:'a. ,and
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. ,(equal(simp_rec_fun(x,f,n,0),x) x:'a. ,(equal(simp_rec_fun(x,f,n,0),x)
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. ,,all x:'a. ,,all
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. ,,( x:'a. ,,( m:hnum. implies m:hnum. implies
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. ,,( x:'a. ,,( m:hnum. (lt(m,n) m:hnum. (lt(m,n)
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. ,,( x:'a. ,,( m:hnum. ,equal m:hnum. ,equal
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. ,,( x:'a. ,,( m:hnum. ,(simp_rec_fun(x,f,n,suc(m)) m:hnum. ,(simp_rec_fun(x,f,n,suc(m))
Thm* ( n:hnum. ( n:hnum. (  'a. ( 'a. ( x:'a. ,,( x:'a. ,,( m:hnum. ,,f(simp_rec_fun(x,f,n,m)))))))))) m:hnum. ,,f(simp_rec_fun(x,f,n,m)))))))))) | [hsimp_rec_fun_lemma] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. implies(lt(m,n),not(equal(m,n))))) n:hnum. implies(lt(m,n),not(equal(m,n))))) | [hless_not_eq] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. implies(equal(m,n),not(lt(m,n))))) n:hnum. implies(equal(m,n),not(lt(m,n))))) | [hnot_less_eq] |
Thm* all( n:hnum. not(equal(suc(n),n))) n:hnum. not(equal(suc(n),n))) | [hsuc_id] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. implies(equal(suc(m),n),lt(m,n)))) n:hnum. implies(equal(suc(m),n),lt(m,n)))) | [heq_less] |
Thm* all( n:hnum. lt(0,suc(n))) n:hnum. lt(0,suc(n))) | [hless_0] |
Thm* all
Thm* ( m:hnum. all m:hnum. all
Thm* ( m:hnum. ( m:hnum. ( n:hnum. implies n:hnum. implies
Thm* ( m:hnum. ( m:hnum. ( n:hnum. (lt(m,suc(n)) n:hnum. (lt(m,suc(n))
Thm* ( m:hnum. ( m:hnum. ( n:hnum. ,implies(not(equal(m,n)),lt(m,n))))) n:hnum. ,implies(not(equal(m,n)),lt(m,n))))) | [hless_suc_imp] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. equal(lt(m,suc(n)),or(equal(m,n),lt(m,n))))) n:hnum. equal(lt(m,suc(n)),or(equal(m,n),lt(m,n))))) | [hless_thm] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. implies(or(equal(m,n),lt(m,n)),lt(m,suc(n))))) n:hnum. implies(or(equal(m,n),lt(m,n)),lt(m,suc(n))))) | [hless_lemma2] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. implies(lt(m,suc(n)),or(equal(m,n),lt(m,n))))) n:hnum. implies(lt(m,suc(n)),or(equal(m,n),lt(m,n))))) | [hless_lemma1] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. implies(lt(m,n),lt(m,suc(n))))) n:hnum. implies(lt(m,n),lt(m,suc(n))))) | [hless_suc] |
Thm* all( n:hnum. lt(n,suc(n))) n:hnum. lt(n,suc(n))) | [hless_suc_refl] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. implies(lt(m,n),lt(suc(m),suc(n))))) n:hnum. implies(lt(m,n),lt(suc(m),suc(n))))) | [hless_mono] |
Thm* all( n:hnum. not(lt(n,0))) n:hnum. not(lt(n,0))) | [hnot_less_0] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. implies(lt(suc(m),n),lt(m,n)))) n:hnum. implies(lt(suc(m),n),lt(m,n)))) | [hsuc_less] |
Thm* all( n:hnum. not(lt(n,n))) n:hnum. not(lt(n,n))) | [hless_refl] |
Thm* all( m:hnum. all( m:hnum. all( n:hnum. equal(equal(suc(m),suc(n)),equal(m,n)))) n:hnum. equal(equal(suc(m),suc(n)),equal(m,n)))) | [hinv_suc_eq] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( x:'a. all x:'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. all 'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( m:hnum. equal m:hnum. equal
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( m:hnum. (prim_rec(x,f,m) m:hnum. (prim_rec(x,f,m)
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ( 'a. ( m:hnum. ,prim_rec_fun(x,f,m,pre(m)))))) m:hnum. ,prim_rec_fun(x,f,m,pre(m)))))) | [hprim_rec_wd] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( x:'a. all x:'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. equal 'a. equal
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. (prim_rec_fun(x,f) 'a. (prim_rec_fun(x,f)
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,simp_rec 'a. ,simp_rec
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,(( 'a. ,(( n:hnum. x) n:hnum. x)
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,, 'a. ,, fun:hnum fun:hnum   'a. 'a.  n:hnum. f n:hnum. f
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,, 'a. ,, fun:hnum fun:hnum   'a. 'a.  n:hnum. (fun(pre(n)) n:hnum. (fun(pre(n))
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   hnum hnum   'a. ,, 'a. ,, fun:hnum fun:hnum   'a. 'a.  n:hnum. ,n))))) n:hnum. ,n))))) | [hprim_rec_fun_wd] |
Thm* all
Thm* ( m:hnum. equal m:hnum. equal
Thm* ( m:hnum. (pre(m) m:hnum. (pre(m)
Thm* ( m:hnum. ,cond(equal(m,0),0,select( m:hnum. ,cond(equal(m,0),0,select( n:hnum. equal(m,suc(n)))))) n:hnum. equal(m,suc(n)))))) | [hpre_def] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( x:'a. all x:'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. all 'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. equal n:hnum. equal
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. (simp_rec(x,f,n) n:hnum. (simp_rec(x,f,n)
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,simp_rec_fun(x,f,suc(n),n))))) n:hnum. ,simp_rec_fun(x,f,suc(n),n))))) | [hsimp_rec_wd] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( x:'a. all x:'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. all 'a. all
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. equal n:hnum. equal
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. (simp_rec_fun(x,f,n) n:hnum. (simp_rec_fun(x,f,n)
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,select n:hnum. ,select
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,( n:hnum. ,( fun:hnum fun:hnum   'a. simp_rec_rel 'a. simp_rec_rel
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,( n:hnum. ,( fun:hnum fun:hnum   'a. (fun 'a. (fun
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,( n:hnum. ,( fun:hnum fun:hnum   'a. ,x 'a. ,x
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,( n:hnum. ,( fun:hnum fun:hnum   'a. ,f 'a. ,f
Thm* ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,( n:hnum. ,( fun:hnum fun:hnum   'a. ,n)))))) 'a. ,n)))))) | [hsimp_rec_fun_wd] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* ( fun:hnum fun:hnum
Thm* (  'a. all 'a. all
Thm* (  'a. ( 'a. ( x:'a. all x:'a. all
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. all 'a. all
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. equal n:hnum. equal
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. (simp_rec_rel(fun,x,f,n) n:hnum. (simp_rec_rel(fun,x,f,n)
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,and n:hnum. ,and
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,(equal(fun(0),x) n:hnum. ,(equal(fun(0),x)
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,,all n:hnum. ,,all
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,,( n:hnum. ,,( m:hnum. implies m:hnum. implies
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,,( n:hnum. ,,( m:hnum. (lt(m,n) m:hnum. (lt(m,n)
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,,( n:hnum. ,,( m:hnum. ,equal m:hnum. ,equal
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,,( n:hnum. ,,( m:hnum. ,(fun(suc(m)) m:hnum. ,(fun(suc(m))
Thm* (  'a. ( 'a. ( x:'a. ( x:'a. ( f:'a f:'a   'a. ( 'a. ( n:hnum. ,,( n:hnum. ,,( m:hnum. ,,f(fun(m))))))))))) m:hnum. ,,f(fun(m))))))))))) | [hsimp_rec_rel_wd] |
Thm* all
Thm* ( m:hnum. all m:hnum. all
Thm* ( m:hnum. ( m:hnum. ( n:hnum. equal n:hnum. equal
Thm* ( m:hnum. ( m:hnum. ( n:hnum. (lt(m,n) n:hnum. (lt(m,n)
Thm* ( m:hnum. ( m:hnum. ( n:hnum. ,exists n:hnum. ,exists
Thm* ( m:hnum. ( m:hnum. ( n:hnum. ,( n:hnum. ,( P:hnum P:hnum   hbool. and hbool. and
Thm* ( m:hnum. ( m:hnum. ( n:hnum. ,( n:hnum. ,( P:hnum P:hnum   hbool. (all hbool. (all
Thm* ( m:hnum. ( m:hnum. ( n:hnum. ,( n:hnum. ,( P:hnum P:hnum   hbool. (( hbool. (( n:hnum. implies(P(suc(n)),P(n))) n:hnum. implies(P(suc(n)),P(n)))
Thm* ( m:hnum. ( m:hnum. ( n:hnum. ,( n:hnum. ,( P:hnum P:hnum   hbool. ,and(P(m),not(P(n)))))))) hbool. ,and(P(m),not(P(n)))))))) | [hless_def] |
Def prim_rec ==  x:'a. x:'a.  f:'a f:'a     'a. 'a.  m: m: . prim_rec_fun(x,f,m,pre(m)) . prim_rec_fun(x,f,m,pre(m)) | [hprim_rec] |
Def prim_rec_fun
Def ==  x:'a. x:'a.  f:'a f:'a     'a. simp_rec 'a. simp_rec
Def ==  x:'a. x:'a.  f:'a f:'a     'a. (( 'a. (( n: n: . x) . x)
Def ==  x:'a. x:'a.  f:'a f:'a     'a. , 'a. , fun: fun:   'a. 'a.  n: n: . f(fun(pre(n)),n)) . f(fun(pre(n)),n)) | [hprim_rec_fun] |
Def pre ==  n: n: . pre(n) . pre(n) | [hpre] |
Def simp_rec ==  x:'a. x:'a.  f:'a f:'a  'a. 'a.  n: n: . ncompose(f;n;x) . ncompose(f;n;x) | [hsimp_rec] |
Def simp_rec_fun
Def ==  x:'a. x:'a.  f:'a f:'a  'a. 'a.  n: n: . @ . @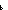 fun: fun:   'a. (simp_rec_rel(fun,x,f,n)) 'a. (simp_rec_rel(fun,x,f,n)) | [hsimp_rec_fun] |
Def simp_rec_rel
Def ==  fun: fun:   'a. 'a.  x:'a. x:'a.  f:'a f:'a  'a. 'a.  n: n: . . 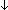 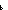 (fun(0) = x (fun(0) = x
Def == & ( m: m: . m<n . m<n 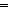 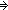 fun(m+1) = f(fun(m)))) fun(m+1) = f(fun(m)))) | [hsimp_rec_rel] |
Def lt ==  m: m: . .  n: n: . m< . m<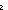 n n | [hlt] |