| | Who Cites hprim rec? |
|
| hprim_rec | Def prim_rec ==  x:'a. x:'a.  f:'a f:'a     'a. 'a.  m: m: . prim_rec_fun(x,f,m,pre(m)) . prim_rec_fun(x,f,m,pre(m)) |
| | | Thm*  'a:S. prim_rec 'a:S. prim_rec  ('a ('a   ('a ('a   hnum hnum   'a) 'a)   hnum hnum   'a) 'a) |
|
| hprim_rec_fun | Def prim_rec_fun
Def ==  x:'a. x:'a.  f:'a f:'a     'a. simp_rec 'a. simp_rec
Def ==  x:'a. x:'a.  f:'a f:'a     'a. (( 'a. (( n: n: . x) . x)
Def ==  x:'a. x:'a.  f:'a f:'a     'a. , 'a. , fun: fun:   'a. 'a.  n: n: . f(fun(pre(n)),n)) . f(fun(pre(n)),n)) |
| | | Thm*  'a:S. prim_rec_fun 'a:S. prim_rec_fun  ('a ('a   ('a ('a   hnum hnum   'a) 'a)   hnum hnum   hnum hnum   'a) 'a) |
|
| pre | Def pre(n) == if n=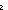 0 then 0 else n-1 fi 0 then 0 else n-1 fi |
| | | Thm*  n: n: . pre(n) . pre(n)   |
|
| hnum | Def hnum ==  |
| | | Thm* hnum  S S |
|
| hsimp_rec | Def simp_rec ==  x:'a. x:'a.  f:'a f:'a  'a. 'a.  n: n: . ncompose(f;n;x) . ncompose(f;n;x) |
| | | Thm*  'a:S. simp_rec 'a:S. simp_rec  ('a ('a   ('a ('a   'a) 'a)   hnum hnum   'a) 'a) |
|
| nat | Def  == {i: == {i: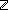 | 0 | 0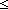 i } i } |
| | | Thm*   Type Type |
| | | Thm*   S S |
|
| tlambda | Def ( x:T. b(x))(x) == b(x) x:T. b(x))(x) == b(x) |
|
| ncompose | Def ncompose(f;n;x) == if n=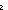 0 then x else f(ncompose(f;n-1;x)) fi (recursive) 0 then x else f(ncompose(f;n-1;x)) fi (recursive) |
| | | Thm*  'a:Type, n: 'a:Type, n: , x:'a, f:('a , x:'a, f:('a  'a). ncompose(f;n;x) 'a). ncompose(f;n;x)  'a 'a |
|
| eq_int | Def i=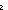 j == if i=j j == if i=j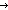 true true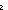 ; false ; false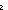 fi fi |
| | | Thm*  i,j: i,j: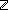 . (i= . (i=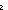 j) j)  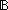 |
|
| bif | Def bif(b; bx.x(bx); by.y(by)) == if b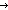 x(*) else y( x(*) else y( x.x) fi x.x) fi |
| | | Thm*  A:Type, b: A:Type, b: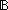 , x:(b , x:(b  A), y:(( A), y:((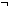 b) b)  A). bif(b; bx.x(bx); by.y(by)) A). bif(b; bx.x(bx); by.y(by))  A A |
|
| hfun | Def 'a   'b == 'a 'b == 'a  'b 'b |
| | | Thm*  'a,'b:S. ('a 'a,'b:S. ('a   'b) 'b)  S S |
|
| le | Def A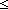 B == B == 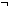 B<A B<A |
| | | Thm*  i,j: i,j: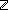 . (i . (i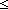 j) j)  Prop Prop |
|
| not | Def 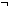 A == A A == A 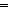 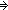 False False |
| | | Thm*  A:Prop. ( A:Prop. (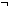 A) A)  Prop Prop |