| | Who Cites decl? |
|
| decl | Def Decl == Label  Type Type |
| | | Thm* Decl{i}  Type{i'} Type{i'} |
|
| ioa_mng | Def [[A]] rho de e == mk_sm([[A.da]] rho, [[A.ds]] rho,  s.[[A.init]] rho A.ds < > de e s s.[[A.init]] rho A.ds < > de e s 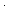 niltrace(), niltrace(),  s1,a,s2. ( s1,a,s2. ( p:pre(). p p:pre(). p  A.pre A.pre   p.kind = kind(a) p.kind = kind(a)   [[p.rel]] rho A.ds dec_lookup(A.da;kind(a)) de e s1 value(a) niltrace()) & ( [[p.rel]] rho A.ds dec_lookup(A.da;kind(a)) de e s1 value(a) niltrace()) & ( ef:eff(). ef ef:eff(). ef  A.eff A.eff   ef.kind = kind(a) ef.kind = kind(a)   s2.ef.smt.lbl = [[ef.smt.term]] 1of(e) s1 value(a) niltrace() s2.ef.smt.lbl = [[ef.smt.term]] 1of(e) s1 value(a) niltrace()  [[ef.smt.typ]] rho) & ( [[ef.smt.typ]] rho) & ( fr:frame(). fr fr:frame(). fr  A.frame A.frame   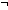 (kind(a) (kind(a)  fr.acts) fr.acts)   s2.fr.var = s1.fr.var s2.fr.var = s1.fr.var  [[fr.typ]] rho)) [[fr.typ]] rho)) |
| | | Thm*  A:ioa{i:l}(), de:sig(), rho:Decl, e:{[[de]] rho}. tc_ioa(A;de) A:ioa{i:l}(), de:sig(), rho:Decl, e:{[[de]] rho}. tc_ioa(A;de)   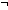 ioa_mentions_trace(A) ioa_mentions_trace(A)   [[A]] rho de e [[A]] rho de e  sm{i:l}() sm{i:l}() |
|
| decls_mng | Def [[ds]] rho == [[d]] rho for d  {d:dec()| d {d:dec()| d  ds } ds } |
| | | Thm*  ds:Collection(dec()), rho:Decl. [[ds]] rho ds:Collection(dec()), rho:Decl. [[ds]] rho  Decl Decl |
|
| ioa | Def ioa{i:l}() == Collection(dec()) Collection(dec()) Collection(dec()) Collection(rel()) Collection(rel()) Collection(pre()) Collection(pre()) Collection(eff()) Collection(eff()) Collection(frame()) Collection(frame()) |
| | | Thm* ioa{i:l}()  Type{i'} Type{i'} |
|
| ioa_all | Def ioa_all(I; i.A(i)) == mk_ioa(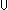 i:I. A(i).ds, i:I. A(i).ds, 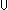 i:I. A(i).da, i:I. A(i).da, 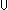 i:I. A(i).init, i:I. A(i).init, 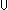 i:I. A(i).pre, i:I. A(i).pre, 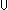 i:I. A(i).eff, i:I. A(i).eff, 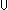 i:I. A(i).frame) i:I. A(i).frame) |
| | | Thm*  I:Type, A:(I I:Type, A:(I  ioa{i:l}()). ioa_all(I; i.A(i)) ioa{i:l}()). ioa_all(I; i.A(i))  ioa{i:l}() ioa{i:l}() |
|
| ioa_ds | Def t.ds == 1of(t) |
| | | Thm*  t:ioa{i:l}(). t.ds t:ioa{i:l}(). t.ds  Collection(dec()) Collection(dec()) |
|
| record_pair | Def {p} == {1of(p)} {2of(p)} {2of(p)} |
| | | Thm*  p:(Decl p:(Decl Decl). {p} Decl). {p}  Type Type |
|
| sm_state | Def M.state == {M.ds} |
| | | Thm*  M:sm{i:l}(). M.state M:sm{i:l}(). M.state  Type Type |
|
| record | Def {d} == l:Label  decl_type(d;l) decl_type(d;l) |
| | | Thm*  d:Decl. {d} d:Decl. {d}  Type Type |
|
| sig | Def sig() == (Label  SimpleType) SimpleType) (Label (Label  (SimpleType List)) (SimpleType List)) |
| | | Thm* sig()  Type Type |
|
| sig_mng | Def [[s]] rho == <  op.[[s.fun(op)]] rho, op.[[s.fun(op)]] rho, R.[[s.rel(R)]] rho > R.[[s.rel(R)]] rho > |
| | | Thm*  s:sig(), rho:Decl{i}. sig_mng{i:l}(s; rho) s:sig(), rho:Decl{i}. sig_mng{i:l}(s; rho)  Decl{i} Decl{i} Decl{i'} Decl{i'} |
|
| dec_lookup | Def dec_lookup(ds;x) == < d.typ | d  < d < d  ds | ds | 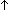 d.lbl = d.lbl =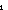 x > > x > > |
| | | Thm*  ds:Collection(dec()), x:Label. dec_lookup(ds;x) ds:Collection(dec()), x:Label. dec_lookup(ds;x)  Collection(SimpleType) Collection(SimpleType) |
|
| dec | Def dec() == Label SimpleType SimpleType |
| | | Thm* dec()  Type Type |
|
| frame | Def frame() == Label SimpleType SimpleType (Label List) (Label List) |
| | | Thm* frame()  Type Type |
|
| eff | Def eff() == Label Label Label SimpleType SimpleType smt() smt() |
| | | Thm* eff()  Type Type |
|
| pre | Def pre() == Label Label Label rel() rel() |
| | | Thm* pre()  Type Type |
|
| pred_mng | Def [[p]] rho ds da de e s a tr ==  r:rel(). r r:rel(). r  p p   [[r]] rho ds da de e s a tr [[r]] rho ds da de e s a tr |
| | | Thm*  p:Fmla, ds,daa:Collection(dec()), da:Collection(SimpleType), de:sig(), rho:Decl, e:{[[de]] rho}, s:{[[ds]] rho}, a:[[da]] rho, tr:trace_env([[daa]] rho). trace_consistent_pred(rho;daa;tr.proj;p) p:Fmla, ds,daa:Collection(dec()), da:Collection(SimpleType), de:sig(), rho:Decl, e:{[[de]] rho}, s:{[[ds]] rho}, a:[[da]] rho, tr:trace_env([[daa]] rho). trace_consistent_pred(rho;daa;tr.proj;p)   tc_pred(p;ds;da;de) tc_pred(p;ds;da;de)   [[p]] rho ds da de e s a tr [[p]] rho ds da de e s a tr  Prop Prop |
|
| rel | Def rel() == relname() (Term List) (Term List) |
| | | Thm* rel()  Type Type |
|
| smt | Def smt() == Label Term Term SimpleType SimpleType |
| | | Thm* smt()  Type Type |
|
| relname | Def relname() == SimpleType+Label |
| | | Thm* relname()  Type Type |
|
| st | Def SimpleType == Tree(Label+Unit) |
| | | Thm* SimpleType  Type Type |
|
| term | Def Term == Tree(ts()) |
| | | Thm* Term  Type Type |
|
| ts | Def ts() == Label+Label+Label+Label+Label |
| | | Thm* ts()  Type Type |
|
| lbl | Def Label == {p:Pattern| 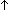 ground_ptn(p) } ground_ptn(p) } |
| | | Thm* Label  Type Type |
|
| dec_mng | Def [[d]] rho == Case(d) Case x : s = > x:[[s]] rho |
| | | Thm*  rho:Decl, d:dec(). [[d]] rho rho:Decl, d:dec(). [[d]] rho  Decl Decl |
|
| col_union | Def (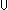 i:I. C(i))(x) == i:I. C(i))(x) == 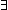 i:I. x i:I. x  C(i) C(i) |
| | | Thm*  T,I:Type, C:(I T,I:Type, C:(I  Collection(T)). ( Collection(T)). (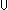 i:I. C(i)) i:I. C(i))  Collection(T) Collection(T) |
|
| col_filter | Def < x  c | P(x) > (x) == x c | P(x) > (x) == x  c & P(x) c & P(x) |
| | | Thm*  T:Type, c:Collection(T), Q:(T T:Type, c:Collection(T), Q:(T  Prop). < i Prop). < i  c | Q(i) > c | Q(i) >  Collection(T) Collection(T) |
|
| col_map | Def < f(x) | x  c > (y) == c > (y) == 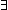 x:T. x x:T. x  c & y = f(x) c & y = f(x)  T' T' |
| | | Thm*  T,T':Type, f:(T T,T':Type, f:(T  T'), c:Collection(T). < f(x) | x T'), c:Collection(T). < f(x) | x  c > c >  Collection(T') Collection(T') |
|
| col_member | Def x  c == c(x) c == c(x) |
| | | Thm*  T:Type, x:T, c:Collection(T). x T:Type, x:T, c:Collection(T). x  c c  Prop Prop |
|
| dall | Def D(i) for i  I(x) == I(x) == 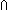 i:I. D(i)(x) i:I. D(i)(x) |
| | | Thm*  I:Type, D:(I I:Type, D:(I  Decl). D(i) for i Decl). D(i) for i  I I  Decl Decl |
|
| col | Def Collection(T) == T  Prop Prop |
| | | Thm*  T:Type{i'}. Collection{i}(T) T:Type{i'}. Collection{i}(T)  Type{i'} Type{i'} |
|
| ioa_frame | Def t.frame == 2of(2of(2of(2of(2of(t))))) |
| | | Thm*  t:ioa{i:l}(). t.frame t:ioa{i:l}(). t.frame  Collection(frame()) Collection(frame()) |
|
| ioa_eff | Def t.eff == 1of(2of(2of(2of(2of(t))))) |
| | | Thm*  t:ioa{i:l}(). t.eff t:ioa{i:l}(). t.eff  Collection(eff()) Collection(eff()) |
|
| ioa_pre | Def t.pre == 1of(2of(2of(2of(t)))) |
| | | Thm*  t:ioa{i:l}(). t.pre t:ioa{i:l}(). t.pre  Collection(pre()) Collection(pre()) |
|
| ioa_init | Def t.init == 1of(2of(2of(t))) |
| | | Thm*  t:ioa{i:l}(). t.init t:ioa{i:l}(). t.init  Collection(rel()) Collection(rel()) |
| | | Thm*  t:ioa{i:l}(). t.init t:ioa{i:l}(). t.init  Fmla Fmla |
|
| ioa_da | Def t.da == 1of(2of(t)) |
| | | Thm*  t:ioa{i:l}(). t.da t:ioa{i:l}(). t.da  Collection(dec()) Collection(dec()) |
|
| mk_ioa | Def mk_ioa(ds, da, init, pre, eff, frame) == < ds,da,init,pre,eff,frame > |
| | | Thm*  ds,da:Collection(dec()), init:Collection(rel()), pre:Collection(pre()), eff:Collection(eff()), frame:Collection(frame()). mk_ioa(ds, da, init, pre, eff, frame) ds,da:Collection(dec()), init:Collection(rel()), pre:Collection(pre()), eff:Collection(eff()), frame:Collection(frame()). mk_ioa(ds, da, init, pre, eff, frame)  ioa{i:l}() ioa{i:l}() |
|
| frame_var | Def t.var == 1of(t) |
| | | Thm*  t:frame(). t.var t:frame(). t.var  Label Label |
|
| frame_typ | Def t.typ == 1of(2of(t)) |
| | | Thm*  t:frame(). t.typ t:frame(). t.typ  SimpleType SimpleType |
|
| rel_mng | Def [[r]] rho ds da de e s a tr == list_accum(x,t.x([[t]] 1of(e) s a tr);[[r.name]] rho 2of(e) ;r.args) |
| | | Thm*  r:rel(), ds,da:Collection(dec()), de:sig(), rho:Decl, st1:Collection(SimpleType), e:{[[de]] rho}, s:{[[ds]] rho}, a:[[st1]] rho, tr:trace_env([[da]] rho). trace_consistent_rel(rho;da;tr.proj;r) r:rel(), ds,da:Collection(dec()), de:sig(), rho:Decl, st1:Collection(SimpleType), e:{[[de]] rho}, s:{[[ds]] rho}, a:[[st1]] rho, tr:trace_env([[da]] rho). trace_consistent_rel(rho;da;tr.proj;r)   tc(r;ds;st1;de) tc(r;ds;st1;de)   [[r]] rho ds st1 de e s a tr [[r]] rho ds st1 de e s a tr  Prop Prop |
| | | Thm*  rho:Decl, ds,daa:Collection(dec()), da1:Collection(SimpleType), de:sig(), s:{[[ds]] rho}, e:{[[de]] rho}, tr:trace_env([[daa]] rho), r:rel(). closed_rel(r) rho:Decl, ds,daa:Collection(dec()), da1:Collection(SimpleType), de:sig(), s:{[[ds]] rho}, e:{[[de]] rho}, tr:trace_env([[daa]] rho), r:rel(). closed_rel(r)   tc(r;ds;da1;de) tc(r;ds;da1;de)   trace_consistent_rel(rho;daa;tr.proj;r) trace_consistent_rel(rho;daa;tr.proj;r)   [[r]] rho ds da1 de e s [[r]] rho ds da1 de e s 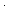 tr tr  Prop Prop |
|
| term_mng | Def [[t]] e s a tr
== iterate(statevar x- > s.x
statevar x'- > s.x
funsymbol f- > e.f
freevar x- > a
trace(P)- > tr.P
x(y)- > x(y)
over t) |
|
| tproj | Def tre.P == tre.trace | tre.proj(P) |
| | | Thm*  d:Decl, tre:trace_env(d), P:Label. tre.P d:Decl, tre:trace_env(d), P:Label. tre.P  ( (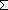 d) List d) List |
|
| trace_projection | Def tr | P == filter( x.P(kind(x));tr) x.P(kind(x));tr) |
| | | Thm*  d:Decl, tr:( d:Decl, tr:(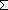 d) List, P:(Label d) List, P:(Label  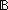 ). tr | P ). tr | P  ( (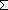 d) List d) List |
|
| kind | Def kind(a) == 1of(a) |
| | | Thm*  d:Decl, a:( d:Decl, a:(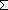 d). kind(a) d). kind(a)  Label Label |
| | | Thm*  M:sm{i:l}(), a:M.action. kind(a) M:sm{i:l}(), a:M.action. kind(a)  Label & kind(a) Label & kind(a)  Pattern Pattern |
|
| smt_term | Def t.term == 1of(2of(t)) |
| | | Thm*  t:smt(). t.term t:smt(). t.term  Term Term |
|
| smt_lbl | Def t.lbl == 1of(t) |
| | | Thm*  t:smt(). t.lbl t:smt(). t.lbl  Label Label |
|
| eff_kind | Def t.kind == 1of(t) |
| | | Thm*  t:eff(). t.kind t:eff(). t.kind  Label Label |
|
| pre_kind | Def t.kind == 1of(t) |
| | | Thm*  t:pre(). t.kind t:pre(). t.kind  Label Label |
|
| sig_fun | Def t.fun == 1of(t) |
| | | Thm*  t:sig(). t.fun t:sig(). t.fun  Label Label  SimpleType SimpleType |
|
| sm_ds | Def t.ds == 1of(2of(t)) |
| | | Thm*  t:sm{i:l}(). t.ds t:sm{i:l}(). t.ds  Decl Decl |
|
| dec_lbl | Def t.lbl == 1of(t) |
| | | Thm*  t:dec(). t.lbl t:dec(). t.lbl  Label Label |
|
| rel_name | Def t.name == 1of(t) |
| | | Thm*  t:rel(). t.name t:rel(). t.name  relname() relname() |
|
| trace_env_trace | Def t.trace == 1of(t) |
| | | Thm*  d:Decl, t:trace_env(d). t.trace d:Decl, t:trace_env(d). t.trace  ( (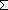 d) List d) List |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| relname_mng | Def [[rn]] rho e == Case(rn) Case eq(Q) = >  x,y. x = y x,y. x = y  [[Q]] rho Case R = > e.R Default = > True [[Q]] rho Case R = > e.R Default = > True |
|
| r_select | Def r.l == r(l) |
| | | Thm*  d:Decl, r:{d}, l:Label. r.l d:Decl, r:{d}, l:Label. r.l  d(l) d(l) |
|
| st_list_mng | Def [[l]] rho == reduce( s,m. [[s]] rho s,m. [[s]] rho  m;Prop;l) m;Prop;l) |
| | | Thm*  l:SimpleType List, rho:Decl{i}. [[l]] rho{i} l:SimpleType List, rho:Decl{i}. [[l]] rho{i}  Type{i'} Type{i'} |
|
| st_mng | Def [[s]] rho == t_iterate(st_lift(rho); x,y. x x,y. x  y;s) y;s) |
| | | Thm*  rho:Decl, s:SimpleType. [[s]] rho rho:Decl, s:SimpleType. [[s]] rho  Type Type |
|
| frame_acts | Def t.acts == 2of(2of(t)) |
| | | Thm*  t:frame(). t.acts t:frame(). t.acts  Label List Label List |
|
| l_member | Def (x  l) == l) == 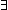 i: i: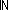 . i < ||l|| & x = l[i] . i < ||l|| & x = l[i]  T T |
| | | Thm*  T:Type, x:T, l:T List. (x T:Type, x:T, l:T List. (x  l) l)  Prop Prop |
|
| nat | Def 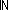 == {i: == {i: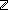 | 0 | 0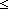 i } i } |
| | | Thm* 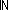  Type Type |
|
| le | Def A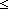 B == B == 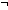 B < A B < A |
| | | Thm*  i,j: i,j: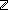 . (i . (i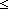 j) j)  Prop Prop |
|
| not | Def 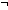 A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. (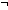 A) A)  Prop Prop |
|
| niltrace | Def niltrace() == mk_trace_env(nil,  P,k. false P,k. false ) ) |
| | | Thm*  d:Decl. niltrace() d:Decl. niltrace()  trace_env(d) trace_env(d) |
|
| value | Def value(a) == 2of(a) |
| | | Thm*  d:Decl, a:( d:Decl, a:(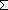 d). value(a) d). value(a)  d(kind(a)) d(kind(a)) |
|
| eff_smt | Def t.smt == 2of(2of(2of(t))) |
| | | Thm*  t:eff(). t.smt t:eff(). t.smt  smt() smt() |
|
| smt_typ | Def t.typ == 2of(2of(t)) |
| | | Thm*  t:smt(). t.typ t:smt(). t.typ  SimpleType SimpleType |
|
| pre_rel | Def t.rel == 2of(2of(t)) |
| | | Thm*  t:pre(). t.rel t:pre(). t.rel  rel() rel() |
|
| col_none | Def < > (x) == False |
| | | Thm*  T:Type. < > T:Type. < >  Collection(T) Collection(T) |
|
| mk_sm | Def mk_sm(da, ds, init, trans) == < da,ds,init,trans > |
| | | Thm*  da,ds:Decl, init:({ds} da,ds:Decl, init:({ds}  Prop), trans:({ds} Prop), trans:({ds}  ( (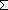 da) da)  {ds} {ds}  Prop). mk_sm(da, ds, init, trans) Prop). mk_sm(da, ds, init, trans)  sm{i:l}() sm{i:l}() |
|
| decl_type | Def decl_type(d;x) == d(x) |
| | | Thm*  dec:Decl, x:Label. decl_type(dec;x) dec:Decl, x:Label. decl_type(dec;x)  Type Type |
|
| sig_rel | Def t.rel == 2of(t) |
| | | Thm*  t:sig(). t.rel t:sig(). t.rel  Label Label  (SimpleType List) (SimpleType List) |
|
| dec_typ | Def t.typ == 2of(t) |
| | | Thm*  t:dec(). t.typ t:dec(). t.typ  SimpleType SimpleType |
|
| rel_args | Def t.args == 2of(t) |
| | | Thm*  t:rel(). t.args t:rel(). t.args  Term List Term List |
|
| trace_env_proj | Def t.proj == 2of(t) |
| | | Thm*  d:Decl, t:trace_env(d). t.proj d:Decl, t:trace_env(d). t.proj  Label Label  Label Label  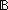 |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 2of(p) B(a)). 2of(p)  B(1of(p)) B(1of(p)) |
|
| ground_ptn | Def ground_ptn(p) == Case(p) Case ptn_var(v) = > false Case ptn_pr( < x, y > ) = > ground_ptn(x) Case ptn_pr( < x, y > ) = > ground_ptn(x)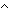  ground_ptn(y) Default = > true ground_ptn(y) Default = > true (recursive) (recursive) |
| | | Thm*  p:Pattern. ground_ptn(p) p:Pattern. ground_ptn(p)  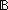 |
|
| assert | Def 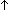 b == if b b == if b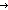 True else False fi True else False fi |
| | | Thm*  b: b: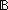 . b . b  Prop Prop |
|
| ptn | Def Pattern == rec(T.ptn_con(T)) |
| | | Thm* Pattern  Type Type |
|
| dbase | Def x:y(a) == if a =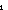 x x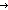 y else Top fi y else Top fi |
| | | Thm*  x:Label, y:Type. x:y x:Label, y:Type. x:y  Decl Decl |
|
| case_mk_dec | Def Case lbl : typ = > body(lbl;typ)(x,z) == x/x2,x1. body(x2;x1) |
|
| term_iter | Def iterate(statevar x- > v(x)
statevar x''- > v'(x')
funsymbol op- > opr(op)
freevar f- > fvar(f)
trace(tr)- > trace(tr)
a(b)- > comb(a;b)
over t)
== term_iterate( x.v(x); x.v(x);
 x'.v'(x'); x'.v'(x');
 op.opr(op); op.opr(op);
 f.fvar(f); f.fvar(f);
 tr.trace(tr); tr.trace(tr);
 a,b. comb(a;b);
t) a,b. comb(a;b);
t) |
| | | Thm*  A:Type, v,v',opr,fvar,trace:(Label A:Type, v,v',opr,fvar,trace:(Label  A), comb:(A A), comb:(A  A A  A), t:Term.
iterate(statevar x- > v(x)
statevar x''- > v'(x')
funsymbol op- > opr(op)
freevar f- > fvar(f)
trace(tr)- > trace(tr)
a(b)- > comb(a,b)
over t) A), t:Term.
iterate(statevar x- > v(x)
statevar x''- > v'(x')
funsymbol op- > opr(op)
freevar f- > fvar(f)
trace(tr)- > trace(tr)
a(b)- > comb(a,b)
over t)
 A A |
|
| term_iterate | Def term_iterate(v;p;op;f;tr;a;t) == t_iterate( x.ts_case(x)var(a)= > v(a)var'(b)= > p(b)opr(c)= > op(c)fvar(d)= > f(d)trace(P)= > tr(P)end_ts_case ;a;t) x.ts_case(x)var(a)= > v(a)var'(b)= > p(b)opr(c)= > op(c)fvar(d)= > f(d)trace(P)= > tr(P)end_ts_case ;a;t) |
| | | Thm*  A:Type, v,op,f,p,tr:(Label A:Type, v,op,f,p,tr:(Label  A), a:(A A), a:(A  A A  A), t:Term. term_iterate(v;p;op;f;tr;a;t) A), t:Term. term_iterate(v;p;op;f;tr;a;t)  A A |
|
| t_iterate | Def t_iterate(l;n;t) == Case(t) Case x;y = > n(t_iterate(l;n;x),t_iterate(l;n;y)) Case tree_leaf(x) = > l(x) Default = > True (recursive) |
| | | Thm*  E,A:Type, l:(E E,A:Type, l:(E  A), n:(A A), n:(A  A A  A), t:Tree(E). t_iterate(l;n;t) A), t:Tree(E). t_iterate(l;n;t)  A A |
|
| eq_lbl | Def l1 =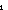 l2 == Case(l1) Case ptn_atom(x) = > Case(l2) Case ptn_atom(y) = > x= l2 == Case(l1) Case ptn_atom(x) = > Case(l2) Case ptn_atom(y) = > x= y y Atom Default = > false Atom Default = > false Case ptn_int(x) = > Case(l2) Case ptn_int(y) = > x= Case ptn_int(x) = > Case(l2) Case ptn_int(y) = > x= y Default = > false y Default = > false Case ptn_var(x) = > Case(l2) Case ptn_var(y) = > x= Case ptn_var(x) = > Case(l2) Case ptn_var(y) = > x= y y Atom Default = > false Atom Default = > false Case ptn_pr( < x, y > ) = > Case(l2) Case ptn_pr( < u, v > ) = > x = Case ptn_pr( < x, y > ) = > Case(l2) Case ptn_pr( < u, v > ) = > x =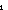 u u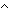  y = y =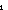 v Default = > false v Default = > false Default = > false Default = > false (recursive) (recursive) |
| | | Thm*  l1,l2:Pattern. l1 = l1,l2:Pattern. l1 =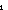 l2 l2  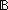 |
|
| ts_case | Def ts_case(x)var(a)= > v(a)var'(b)= > p(b)opr(f)= > op(f)fvar(x)= > f(x)trace(P)= > t(P)end_ts_case == Case(x) Case ts_var(a) = > v(a) Case ts_pvar(b) = > p(b) Case ts_op(f) = > op(f) Case ts_fvar(x) = > f(x) Case ts_trace(P) = > t(P) Default = > 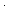 |
| | | Thm*  A:Type, v,op,f,p,t:(Label A:Type, v,op,f,p,t:(Label  A), x:ts(). ts_case(x)var(a)= > v(a)var'(b)= > p(b)opr(f)= > op(f)fvar(y)= > f(y)trace(P)= > t(P)end_ts_case A), x:ts(). ts_case(x)var(a)= > v(a)var'(b)= > p(b)opr(f)= > op(f)fvar(y)= > f(y)trace(P)= > t(P)end_ts_case  A A |
|
| case | Def Case(value) body == body(value,value) |
|
| st_lift | Def st_lift(rho)(x) == InjCase(x; x'. rho(x'); a. Top) |
| | | Thm*  rho:(Label rho:(Label  Type). st_lift(rho) Type). st_lift(rho)  (Label+Unit) (Label+Unit)  Type Type |
|
| select | Def l[i] == hd(nth_tl(i;l)) |
| | | Thm*  A:Type, l:A List, n: A:Type, l:A List, n: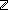 . 0 . 0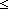 n n   n < ||l|| n < ||l||   l[n] l[n]  A A |
|
| length | Def ||as|| == Case of as; nil 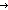 0 ; a.as' 0 ; a.as' 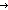 ||as'||+1 (recursive) ||as'||+1 (recursive) |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||  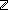 |
| | | Thm* ||nil||  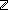 |
|
| mk_trace_env | Def mk_trace_env(trace, proj) == < trace,proj > |
| | | Thm*  d:Decl, trace:( d:Decl, trace:(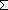 d) List, proj:(Label d) List, proj:(Label  Label Label  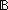 ). mk_trace_env(trace, proj) ). mk_trace_env(trace, proj)  trace_env(d) trace_env(d) |
|
| list_accum | Def list_accum(x,a.f(x;a);y;l) == Case of l; nil 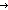 y ; b.l' y ; b.l' 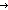 list_accum(x,a.f(x;a);f(y;b);l') (recursive) list_accum(x,a.f(x;a);f(y;b);l') (recursive) |
|
| tree | Def Tree(E) == rec(T.tree_con(E;T)) |
| | | Thm*  E:Type. Tree(E) E:Type. Tree(E)  Type Type |
|
| filter | Def filter(P;l) == reduce( a,v. if P(a) a,v. if P(a)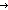 [a / v] else v fi;nil;l) [a / v] else v fi;nil;l) |
| | | Thm*  T:Type, P:(T T:Type, P:(T  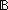 ), l:T List. filter(P;l) ), l:T List. filter(P;l)  T List T List |
|
| reduce | Def reduce(f;k;as) == Case of as; nil 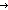 k ; a.as' k ; a.as' 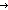 f(a,reduce(f;k;as')) (recursive) f(a,reduce(f;k;as')) (recursive) |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B B  B), k:B, as:A List. reduce(f;k;as) B), k:B, as:A List. reduce(f;k;as)  B B |
|
| case_default | Def Default = > body(value,value) == body |
|
| band | Def p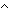  q == if p q == if p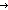 q else false q else false fi fi |
| | | Thm*  p,q: p,q: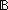 . (p . (p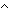  q) q)  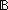 |
|
| case_lbl_pair | Def Case ptn_pr( < x, y > ) = > body(x;y) cont(x1,z) == InjCase(x1; _. cont(z,z); x2. InjCase(x2; _. cont(z,z); x2@0. InjCase(x2@0; _. cont(z,z); x2@1. x2@1/x3,x2@2. body(x3;x2@2)))) |
|
| case_ptn_var | Def Case ptn_var(x) = > body(x) cont(x1,z) == ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) |
|
| ptn_con | Def ptn_con(T) == Atom+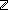 +Atom+(T +Atom+(T T) T) |
| | | Thm*  T:Type. ptn_con(T) T:Type. ptn_con(T)  Type Type |
|
| top | Def Top == Void given Void |
| | | Thm* Top  Type Type |
|
| case_tree_leaf | Def Case tree_leaf(x) = > body(x) cont(x1,z) == InjCase(x1; x2. body(x2); _. cont(z,z)) |
|
| case_node | Def Case x;y = > body(x;y) cont(x1,z) == InjCase(x1; _. cont(z,z); x2. x2/x3,x2@0. body(x3;x2@0)) |
|
| nth_tl | Def nth_tl(n;as) == if n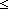  0 0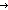 as else nth_tl(n-1;tl(as)) fi (recursive) as else nth_tl(n-1;tl(as)) fi (recursive) |
| | | Thm*  A:Type, as:A List, i: A:Type, as:A List, i: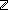 . nth_tl(i;as) . nth_tl(i;as)  A List A List |
|
| case_ptn_int | Def Case ptn_int(x) = > body(x) cont(x1,z) == ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) |
|
| case_relname_other | Def Case x = > body(x) cont(x1,z) == ( x1.inr(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x1]) x1.inr(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x1]) |
|
| case_ts_trace | Def Case ts_trace(x) = > body(x) cont(x1,z) == ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) x1.inr(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) |
|
| case_ts_fvar | Def Case ts_fvar(x) = > body(x) cont(x1,z) == ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) |
|
| case_ts_op | Def Case ts_op(x) = > body(x) cont(x1,z) == ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) |
|
| case_ts_pvar | Def Case ts_pvar(x) = > body(x) cont(x1,z) == ( x1.inr(x2) = > ( x1.inr(x2) = > ( x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) x1.inl(x2) = > body(hd([x2 / tl(x1)])) cont(hd(x1),z))([x2 / tl(x1)]) cont(hd(x1),z))([x1]) |
|
| hd | Def hd(l) == Case of l; nil 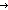 "?" ; h.t "?" ; h.t 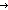 h h |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||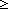 1 1   hd(l) hd(l)  A A |
| | | Thm*  A:Type, l:A List A:Type, l:A List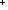 . hd(l) . hd(l)  A A |
|
| eq_atom | Def x= y y Atom == if x=y Atom == if x=y Atom Atom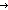 true true ; false ; false fi fi |
| | | Thm*  x,y:Atom. x= x,y:Atom. x= y y Atom Atom  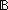 |
|
| eq_int | Def i= j == if i=j j == if i=j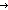 true true ; false ; false fi fi |
| | | Thm*  i,j: i,j: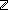 . (i= . (i= j) j)  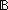 |
|
| case_ptn_atom | Def Case ptn_atom(x) = > body(x) cont(x1,z) == InjCase(x1; x2. body(x2); _. cont(z,z)) |
|
| case_relname_eq | Def Case eq(x) = > body(x) cont(x1,z) == InjCase(x1; x2. body(x2); _. cont(z,z)) |
|
| tree_con | Def tree_con(E;T) == E+(T T) T) |
| | | Thm*  E,T:Type. tree_con(E;T) E,T:Type. tree_con(E;T)  Type Type |
|
| tl | Def tl(l) == Case of l; nil 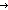 nil ; h.t nil ; h.t 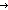 t t |
| | | Thm*  A:Type, l:A List. tl(l) A:Type, l:A List. tl(l)  A List A List |
|
| case_inl | Def inl(x) = > body(x) cont(value,contvalue) == InjCase(value; x. body(x); _. cont(contvalue,contvalue)) |
|
| case_inr | Def inr(x) = > body(x) cont(value,contvalue) == InjCase(value; _. cont(contvalue,contvalue); x. body(x)) |
|
| le_int | Def i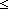  j == j == 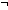  j < j <  i i |
| | | Thm*  i,j: i,j: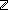 . (i . (i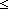  j) j)  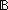 |
|
| lt_int | Def i <  j == if i < j j == if i < j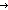 true true ; false ; false fi fi |
| | | Thm*  i,j: i,j: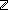 . (i < . (i <  j) j)  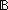 |
|
| bnot | Def 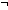  b == if b b == if b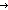 false false else true else true fi fi |
| | | Thm*  b: b: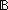 . . 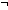  b b  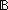 |
|
| case_ts_var | Def Case ts_var(x) = > body(x) cont(x1,z) == InjCase(x1; x2. body(x2); _. cont(z,z)) |