| | Some definitions of interest. |
|
| le | Def A B == B == 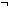 B<A B<A |
| | | Thm*  i,j: i,j: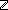 . (i . (i j) j)  Prop Prop |
|
| nth_tl | Def nth_tl(n;as) == if n 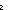 0 0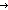 as else nth_tl(n-1;tl(as)) fi (recursive) as else nth_tl(n-1;tl(as)) fi (recursive) |
| | | Thm*  A:Type, as:A List, i: A:Type, as:A List, i: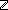 . nth_tl(i;as) . nth_tl(i;as)  A List A List |
|
| le_int | Def i 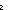 j == j == 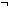 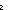 j< j<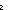 i i |
| | | Thm*  i,j: i,j: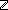 . (i . (i 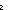 j) j)  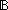 |
|
| length | Def ||as|| == Case of as; nil 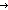 0 ; a.as' 0 ; a.as' 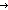 ||as'||+1 (recursive) ||as'||+1 (recursive) |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||  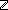 |
| | | Thm* ||nil||  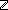 |
|
| lt_int | Def i<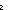 j == if i<j j == if i<j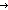 true true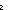 ; false ; false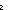 fi fi |
| | | Thm*  i,j: i,j: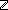 . (i< . (i<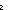 j) j)  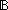 |
|
| tl | Def tl(l) == Case of l; nil 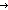 nil ; h.t nil ; h.t 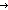 t t |
| | | Thm*  A:Type, l:A List. tl(l) A:Type, l:A List. tl(l)  A List A List |
|
| top | Def Top == Void given Void |
| | | Thm* Top  Type Type |