| | Some definitions of interest. |
|
| world | Def World
Def == T:Id  Id Id  Type Type
Def ==  TA:Id TA:Id  Id Id  Type Type
Def ==  M:IdLnk M:IdLnk  Id Id  Type Type
Def ==  (i:Id (i:Id     (x:Id (x:Id  T(i,x))) T(i,x))) (i:Id (i:Id     action(w-action-dec(TA;M;i))) action(w-action-dec(TA;M;i)))
Def == (i:Id     ({m:Msg(M)| source(mlnk(m)) = i } List)) ({m:Msg(M)| source(mlnk(m)) = i } List)) Top Top |
| | | Thm* World  Type{i'} Type{i'} |
|
| IdLnk | Def IdLnk == Id Id Id  |
| | | Thm* IdLnk  Type Type |
|
| w-snds | Def snds(l;t) == concat(map( t1.m(l;t1);upto(t))) t1.m(l;t1);upto(t))) |
|
| concat | Def concat(ll) == reduce( l,l'. l @ l';nil;ll) l,l'. l @ l';nil;ll) |
| | | Thm*  T:Type, ll:(T List) List. concat(ll) T:Type, ll:(T List) List. concat(ll)  T List T List |
|
| upto | Def upto(n) == if n= 0 0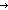 nil else upto(n-1) @ [(n-1)] fi (recursive) nil else upto(n-1) @ [(n-1)] fi (recursive) |
| | | Thm*  n: n: . upto(n) . upto(n)   n List n List |
|
| append | Def as @ bs == Case of as; nil 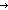 bs ; a.as' bs ; a.as' 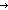 [a / (as' @ bs)] (recursive) [a / (as' @ bs)] (recursive) |
| | | Thm*  T:Type, as,bs:T List. (as @ bs) T:Type, as,bs:T List. (as @ bs)  T List T List |
|
| lsrc | Def source(l) == 1of(l) |
| | | Thm*  l:IdLnk. source(l) l:IdLnk. source(l)  Id Id |
|
| map | Def map(f;as) == Case of as; nil 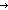 nil ; a.as' nil ; a.as'  [(f(a)) / map(f;as')] [(f(a)) / map(f;as')]
Def (recursive) |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B), l:A List. map(f;l) B), l:A List. map(f;l)  B List B List |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B), l:A List B), l:A List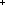 . map(f;l) . map(f;l)  B List B List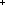 |
|
| w-onlnk | Def onlnk(l;mss) == filter( ms.mlnk(ms) = l;mss) ms.mlnk(ms) = l;mss) |
|
| nat | Def  == {i: == {i: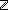 | 0 | 0 i } i } |
| | | Thm*   Type Type |
|
| top | Def Top == Void given Void |
| | | Thm* Top  Type Type |
|
| w-m | Def m(i;t) == 1of(2of(2of(2of(2of(2of(w))))))(i,t) |