| | Who Cites dequiv? |
|
| dequiv | Def DecidableEquiv == T:Type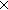 E:T E:T  T T  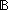 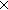 EquivRel(T)( EquivRel(T)( (_1 E _2)) (_1 E _2))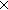 Top Top |
| | | Thm* DecidableEquiv  Type{i'} Type{i'} |
|
| top |
Def Top == Void given Void |
| | |
Thm* Top  Type Type |
|
| assert |
Def  b == if b b == if b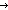 True else False fi True else False fi |
| | | Thm*  b: b: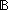 . b . b  Prop Prop |
|
| equiv_rel |
Def EquivRel x,y:T. E(x;y)
== Refl(T;x,y.E(x;y)) & Sym x,y:T. E(x;y) & Trans x,y:T. E(x;y) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). (EquivRel x,y:T. E(x,y)) Prop). (EquivRel x,y:T. E(x,y))  Prop Prop |
|
| trans |
Def Trans x,y:T. E(x;y) ==  a,b,c:T. E(a;b) a,b,c:T. E(a;b)   E(b;c) E(b;c)   E(a;c) E(a;c) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Trans x,y:T. E(x,y) Prop). Trans x,y:T. E(x,y)  Prop Prop |
|
| sym |
Def Sym x,y:T. E(x;y) ==  a,b:T. E(a;b) a,b:T. E(a;b)   E(b;a) E(b;a) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Sym x,y:T. E(x,y) Prop). Sym x,y:T. E(x,y)  Prop Prop |
|
| refl |
Def Refl(T;x,y.E(x;y)) ==  a:T. E(a;a) a:T. E(a;a) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Refl(T;x,y.E(x,y)) Prop). Refl(T;x,y.E(x,y))  Prop Prop |