| 1 | 4.  is-send(E)(x[(i+1)]) is-send(E)(x[(i+1)])
5. is-send(E)(x[i])   loc(E)(x[i]) = loc(E)(x[(i+1)]) loc(E)(x[i]) = loc(E)(x[(i+1)])
6. ||swap(x;i;i+1)|| = ||x||  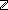
7.  i,j,k: i,j,k: ||x||.
i < j ||x||.
i < j   is-send(E)(x[i])
is-send(E)(x[i])   is-send(E)(x[j])
is-send(E)(x[j])  
 tag(E)(x[i]) = tag(E)(x[j]) tag(E)(x[i]) = tag(E)(x[j])   (x[j] =msg=(E) x[k]) &
(x[j] =msg=(E) x[k]) &  is-send(E)(x[k]) is-send(E)(x[k])   (
( k': k': ||x||. k' < k & (x[i] =msg=(E) x[k']) & ||x||. k' < k & (x[i] =msg=(E) x[k']) &  is-send(E)(x[k']) & loc(E)(x[k']) = loc(E)(x[k])) is-send(E)(x[k']) & loc(E)(x[k']) = loc(E)(x[k]))
8. i@0:  ||swap(x;i;i+1)|| ||swap(x;i;i+1)||
9. j:  ||swap(x;i;i+1)|| ||swap(x;i;i+1)||
10. k:  ||swap(x;i;i+1)|| ||swap(x;i;i+1)||
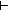 i@0 < j i@0 < j   is-send(E)(x[((i, i+1)(i@0))])
is-send(E)(x[((i, i+1)(i@0))])   is-send(E)(x[((i, i+1)(j))])
is-send(E)(x[((i, i+1)(j))])  
 tag(E)(x[((i, i+1)(i@0))]) = tag(E)(x[((i, i+1)(j))]) tag(E)(x[((i, i+1)(i@0))]) = tag(E)(x[((i, i+1)(j))])   (x[((i, i+1)(j))] =msg=(E) x[((i, i+1)(k))]) &
(x[((i, i+1)(j))] =msg=(E) x[((i, i+1)(k))]) &  is-send(E)(x[((i, i+1)(k))]) is-send(E)(x[((i, i+1)(k))])   (
( k': k': ||swap(x;i;i+1)||.
k' < k
& (x[((i, i+1)(i@0))] =msg=(E) x[((i, i+1)(k'))]) & ||swap(x;i;i+1)||.
k' < k
& (x[((i, i+1)(i@0))] =msg=(E) x[((i, i+1)(k'))]) &  is-send(E)(x[((i, i+1)(k'))])
& loc(E)(x[((i, i+1)(k'))]) = loc(E)(x[((i, i+1)(k))])) is-send(E)(x[((i, i+1)(k'))])
& loc(E)(x[((i, i+1)(k'))]) = loc(E)(x[((i, i+1)(k))])) |