Thm*  L:T List, P:(T L:T List, P:(T  T T  Prop). Prop).
Thm* ( x,y:T. Dec(P(x,y))) x,y:T. Dec(P(x,y)))
Thm*  
Thm* ( x,y:T. x,y:T.  P(x,y) P(x,y)   P(y,x)) P(y,x))
Thm*  
Thm* ( L':T List. L':T List.
Thm* ((L (swap adjacent[ P(x,y)]^*) L') & ( P(x,y)]^*) L') & ( i: i: (||L'||-1). P(L'[i],L'[(i+1)]))) (||L'||-1). P(L'[i],L'[(i+1)]))) | [partial_sort] |
Thm*  L:T List, P:(T L:T List, P:(T  T T  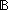 ). ).
Thm* ( x,y:T. P(x,y) x,y:T. P(x,y)    P(y,x)) P(y,x))
Thm*  
Thm* ( L':T List. L':T List.
Thm* ((L guarded_permutation(T;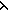 L,i. P(L[i],L[(i+1)])) L') L,i. P(L[i],L[(i+1)])) L')
Thm* (& ( i: i: (||L'||-1). (||L'||-1).  P(L'[i],L'[(i+1)]))) P(L'[i],L'[(i+1)]))) | [partial_sort_exists_2] |
Thm*  L:T List, P:(T L:T List, P:(T  T T  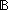 ), n: ), n: (||L||-1). (||L||-1).
Thm* count(x < y in swap(L;n;n+1) | P(x,y))
Thm* =
Thm* count(x < y in L | P(x,y))+if P(L[n],L[(n+1)])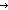 -1 else 0 fi+if P(L[(n+1)] -1 else 0 fi+if P(L[(n+1)]
Thm* count(x < y in L | P(x,y))+if P(L[n],L[(n+1)]) -1 else 0 fi+if P,L[n]) -1 else 0 fi+if P,L[n])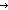
Thm* count(x < y in L | P(x,y))+if P(L[n],L[(n+1)]) -1 else 0 fi+if 1 -1 else 0 fi+if 1
Thm* count(x < y in L | P(x,y))+if P(L[n],L[(n+1)]) -1 else 0 fi+else 0 fi -1 else 0 fi+else 0 fi | [count_pairs_swap] |
Thm*  R:(T R:(T  T T  Prop), k: Prop), k: , x,y:T. , x,y:T.
Thm* (x R^k y)
Thm* 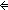 
Thm* ( L:T List. L:T List.
Thm* (||L|| = k+1   & L[0] = x & last(L) = y & ( & L[0] = x & last(L) = y & ( i: i: k. L[i] R L[(i+1)])) k. L[i] R L[(i+1)])) | [rel_exp_list] |
Thm*  L:T List, i: L:T List, i: (||L||-1), a,b:T. (||L||-1), a,b:T.
Thm* a before b  swap(L;i;i+1) swap(L;i;i+1)   a before b a before b  L L 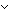 a = L[(i+1)] & b = L[i] a = L[(i+1)] & b = L[i] | [l_before_swap] |
Thm*  i: i: , L:A List. , L:A List.
Thm* i+1<||L||
Thm*  
Thm* ( X,Y:A List. X,Y:A List.
Thm* (L = (X @ [L[i]; L[(i+1)]] @ Y)
Thm* (& swap(L;i;i+1) = (X @ [L[(i+1)]; L[i]] @ Y)) | [swap_adjacent_decomp] |
Thm*  L1,L2:T List, i,j: L1,L2:T List, i,j: ||L1||. ||L1||.
Thm* L2 = swap(L1;i;j)
Thm*  
Thm* L2[i] = L1[j] & L2[j] = L1[i] & ||L2|| = ||L1||   & L1 = swap(L2;i;j) & L1 = swap(L2;i;j)
Thm* & ( x: x: ||L2||. ||L2||.  x = i x = i    x = j x = j   L2[x] = L1[x]) L2[x] = L1[x]) | [swapped_select] |
Thm*  L:T List, i,j,x: L:T List, i,j,x: ||L||. swap(L;i;j)[x] = L[((i, j)(x))] ||L||. swap(L;i;j)[x] = L[((i, j)(x))] | [swap_select] |
Thm*  L:T List, f:( L:T List, f:( ||L|| ||L||   ||L||), i: ||L||), i: ||L||. (L o f)[i] = L[(f(i))] ||L||. (L o f)[i] = L[(f(i))] | [permute_list_select] |
Def swap adjacent[P(x;y)](L1,L2)
Def ==  i: i: (||L1||-1). P(L1[i];L1[(i+1)]) & L2 = swap(L1;i;i+1) (||L1||-1). P(L1[i];L1[(i+1)]) & L2 = swap(L1;i;i+1)  A List A List | [swap_adjacent] |
Def count(x < y in L | P(x;y))
Def == sum(if (i<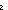 j) j)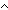 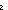 P(L[i];L[j]) P(L[i];L[j])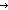 1 else 0 fi | i < ||L||; j < ||L||) 1 else 0 fi | i < ||L||; j < ||L||) | [count_pairs] |
Def (L o f) == mklist(||L||;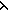 i.L[(f(i))]) i.L[(f(i))]) | [permute_list] |
Def interleaving_occurence(T;L1;L2;L;f1;f2)
Def == ||L|| = ||L1||+||L2||  
Def == & increasing(f1;||L1||) & ( j: j: ||L1||. L1[j] = L[(f1(j))] ||L1||. L1[j] = L[(f1(j))]  T) T)
Def == & increasing(f2;||L2||) & ( j: j: ||L2||. L2[j] = L[(f2(j))] ||L2||. L2[j] = L[(f2(j))]  T) T)
Def == & ( j1: j1: ||L1||, j2: ||L1||, j2: ||L2||. ||L2||.  f1(j1) = f2(j2) f1(j1) = f2(j2)   ) ) | [interleaving_occurence] |
Def disjoint_sublists(T;L1;L2;L)
Def ==  f1:( f1:( ||L1|| ||L1||   ||L||), f2:( ||L||), f2:( ||L2|| ||L2||   ||L||). ||L||).
Def == increasing(f1;||L1||) & ( j: j: ||L1||. L1[j] = L[(f1(j))] ||L1||. L1[j] = L[(f1(j))]  T) T)
Def == & increasing(f2;||L2||) & ( j: j: ||L2||. L2[j] = L[(f2(j))] ||L2||. L2[j] = L[(f2(j))]  T) T)
Def == & ( j1: j1: ||L1||, j2: ||L1||, j2: ||L2||. ||L2||.  f1(j1) = f2(j2)) f1(j1) = f2(j2)) | [disjoint_sublists] |
Def sublist_occurence(T;L1;L2;f)
Def == increasing(f;||L1||) & ( j: j: ||L1||. L1[j] = L2[(f(j))] ||L1||. L1[j] = L2[(f(j))]  T) T) | [sublist_occurence] |