| 2 |
1. T : Type
2. R : T  T T  Prop Prop
3. k : 
4. 0<k
5.  x,y:T. x,y:T.
5. (x R^k-1 y)
5. 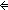 
5. ( L:T List. L:T List.
5. (||L|| = k-1+1   & L[0] = x & last(L) = y & ( & L[0] = x & last(L) = y & ( i: i: (k-1). L[i] R L[(i+1)])) (k-1). L[i] R L[(i+1)]))
  x,y:T. x,y:T.
 (x if k= (x if k=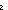 0 0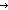 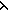 x,y. x = y else x,y. x = y else 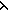 x,y. x,y.  z:T. (x R z) & (z R^k-1 y) fi y) z:T. (x R z) & (z R^k-1 y) fi y)
 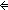 
 ( ( L:T List. L:T List.
 (||L|| = k+1 (||L|| = k+1   & L[0] = x & last(L) = y & ( & L[0] = x & last(L) = y & ( i: i: k. L[i] R L[(i+1)])) k. L[i] R L[(i+1)]))
 | 23 steps |