| 1 | 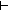 ( (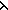 l.Auto(l) l.Auto(l)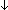 ) ) 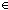 (x,y:Alph*//((Result(Auto)x) = (Result(Auto)y))) (x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)))   |
| 2 | 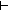 Fin(x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)))
& ( Fin(x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)))
& ( l:Alph*. L(l) l:Alph*. L(l)   ( (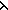 l.Auto(l) l.Auto(l)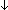 )(l))
& ( )(l))
& ( x,y,z:Alph*. (Result(Auto)x) = (Result(Auto)y) x,y,z:Alph*. (Result(Auto)x) = (Result(Auto)y)   (Result(Auto)z @ x) = (Result(Auto)z @ y)) (Result(Auto)z @ x) = (Result(Auto)z @ y)) |
| 3 | 9. g: (x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)))  
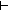 (Fin(x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)))
& ( (Fin(x,y:Alph*//((Result(Auto)x) = (Result(Auto)y)))
& ( l:Alph*. L(l) l:Alph*. L(l)   g(l))
& ( g(l))
& ( x,y,z:Alph*. (Result(Auto)x) = (Result(Auto)y) x,y,z:Alph*. (Result(Auto)x) = (Result(Auto)y)   (Result(Auto)z @ x) = (Result(Auto)z @ y))) (Result(Auto)z @ x) = (Result(Auto)z @ y)))
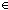 Prop Prop |