At: mn 23 Rl equal Rg 1 5
1. Alph: Type
2. L: Alph*
 Prop
Prop
3. R: Alph*
 Alph*
Alph*
 Prop
Prop
4. EquivRel x,y:Alph*. x R y
5.  x,y,z:Alph*. (x R y)
x,y,z:Alph*. (x R y) 
 ((z @ x) R (z @ y))
((z @ x) R (z @ y))
6. g: (x,y:Alph*//(x R y))


7.  l:Alph*. L(l)
l:Alph*. L(l) 
 g(l)
g(l)
8. Alph* = Alph*
9. x: Alph*
10. y: Alph*
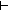 (x L-induced Equiv y)
(x L-induced Equiv y) 
 (x Rg y)
(x Rg y)
By: Inst
Thm*  R:(A*
R:(A*
 A*
A*
 Prop).
(EquivRel x,y:A*. x R y)
Prop).
(EquivRel x,y:A*. x R y) 
 (
( x,y,z:A*. (x R y)
x,y,z:A*. (x R y) 
 ((z @ x) R (z @ y)))
((z @ x) R (z @ y))) 
 (
( g:((x,y:A*//(x R y))
g:((x,y:A*//(x R y))

 ), L:LangOver(A).
(
), L:LangOver(A).
( l:A*. L(l)
l:A*. L(l) 
 g(l))
g(l)) 
 (
( x,y:A*. (x L-induced Equiv y)
x,y:A*. (x L-induced Equiv y) 
 (x Rg y)))
[Alph;R;g;L;x;y]
(x Rg y)))
[Alph;R;g;L;x;y]
Generated subgoal:| 1 | 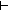 L L 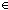 LangOver(Alph) LangOver(Alph) |
About: