| 1 | 13. TBL: ((x,y:Alph*//(x R y))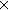 (x,y:Alph*//(x R y)))* (x,y:Alph*//(x R y)))*
14.  s:((x,y:Alph*//(x R y)) s:((x,y:Alph*//(x R y))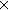 (x,y:Alph*//(x R y))).
mem_f((x,y:Alph*//(x R y)) (x,y:Alph*//(x R y))).
mem_f((x,y:Alph*//(x R y))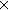 (x,y:Alph*//(x R y));s;TBL) (x,y:Alph*//(x R y));s;TBL)
  (
( w:Alph*.
mem_f((x,y:Alph*//(x R y)) w:Alph*.
mem_f((x,y:Alph*//(x R y))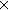 (x,y:Alph*//(x R y));( < (x,y:Alph*//(x R y)) (x,y:Alph*//(x R y));( < (x,y:Alph*//(x R y))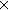 (x,y:Alph*//(x R y))
, (x,y:Alph*//(x R y))
,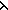 a,xy. xy/x,y. < a.x,a.y > > :w a,xy. xy/x,y. < a.x,a.y > > :w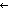 s);fL)) s);fL))
15. x: x,y:Alph*//(x R y)
16. y: x,y:Alph*//(x R y)
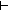 Dec(x Rg y) Dec(x Rg y) |