| 1 |   i: i: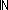 (||map( (||map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ]||-1). c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ]||-1).
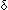 NDA
(1of((map( NDA
(1of((map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[i])
,hd(rev(2of((map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[i])
,hd(rev(2of((map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[i])))
,1of((map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[i])))
,1of((map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[(i+1)]))
& 2of((map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[(i+1)]))
& 2of((map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[(i+1)])
=
rev(tl(rev(2of((map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[(i+1)])
=
rev(tl(rev(2of((map( c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[i])))) c. < 1of(c),a.2of(c) > ;C) @ [ < p,nil > ])[i]))))
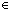 Alph* Alph* |