Thm*  n: n: . CoPrime(fib(n),fib(n+1)) . CoPrime(fib(n),fib(n+1)) | [fib_coprime] |
Thm*  n: n: . fib(n) . fib(n) 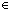  | [fib_wf] |
Thm*  r: r:  , s:{s': , s:{s':  | CoPrime(r,s') }, a,b: | CoPrime(r,s') }, a,b: . .
Thm* 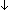  x: x: . ((x = a mod r) & (x = b mod s)) . ((x = a mod r) & (x = b mod s)) | [chrem_exists_a] |
Thm*  r,s: r,s:  . CoPrime(r,s) . CoPrime(r,s)   ( ( a,b: a,b: . .  x: x: . (x = a mod r) & (x = b mod s)) . (x = a mod r) & (x = b mod s)) | [chrem_exists] |
Thm*  r: r:  , s:{s': , s:{s':  | CoPrime(r,s') }. | CoPrime(r,s') }. 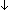  x: x: . ((x = 1 mod r) & (x = 0 mod s)) . ((x = 1 mod r) & (x = 0 mod s)) | [chrem_exists_aux_a] |
Thm*  r,s: r,s:  . CoPrime(r,s) . CoPrime(r,s)   ( ( x: x: . (x = 1 mod r) & (x = 0 mod s)) . (x = 1 mod r) & (x = 0 mod s)) | [chrem_exists_aux] |
Thm*  m,a,a',b,b': m,a,a',b,b': . (a = a' mod m) . (a = a' mod m)   (b = b' mod m) (b = b' mod m)   ((a ((a b) = (a' b) = (a' b') mod m) b') mod m) | [multiply_functionality_wrt_eqmod] |
Thm*  m,a,a',b,b': m,a,a',b,b': . (a = a' mod m) . (a = a' mod m)   (b = b' mod m) (b = b' mod m)   ((a+b) = (a'+b') mod m) ((a+b) = (a'+b') mod m) | [add_functionality_wrt_eqmod] |
Thm*  m,a,a',b,b': m,a,a',b,b': . .
Thm* (a = a' mod m)   (b = b' mod m) (b = b' mod m)   ((a = b mod m) ((a = b mod m)   (a' = b' mod m)) (a' = b' mod m)) | [eqmod_fun] |
Thm*  m,m',a,a',b,b': m,m',a,a',b,b': . .
Thm* m = m'
Thm*  
Thm* (a = a' mod m)   (b = b' mod m) (b = b' mod m)   ((a = b mod m) ((a = b mod m)   (a' = b' mod m')) (a' = b' mod m')) | [eqmod_functionality_wrt_eqmod] |
Thm*  m,a,b: m,a,b: . (a = b mod m) . (a = b mod m)   (b = a mod m) (b = a mod m) | [eqmod_inversion] |
Thm*  m,a,b,c: m,a,b,c: . (a = b mod m) . (a = b mod m)   (b = c mod m) (b = c mod m)   (a = c mod m) (a = c mod m) | [eqmod_transitivity] |
Thm*  m,a,b: m,a,b: . a = b . a = b   (a = b mod m) (a = b mod m) | [eqmod_weakening] |
Thm*  p: p: . prime(p) . prime(p)   ( ( a1,a2: a1,a2: . p | a1 . p | a1 a2 a2   p | a1 p | a1 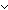 p | a2) p | a2) | [prime_divs_prod] |
Thm*  a: a: . atomic(a) . atomic(a)   prime(a) prime(a) | [atomic_imp_prime] |
Thm*  a1,a2,b: a1,a2,b: . CoPrime(a1,a2) . CoPrime(a1,a2)   a1 | b a1 | b   a2 | b a2 | b   a1 a1 a2 | b a2 | b | [coprime_divisors_prod] |
Thm*  a,b1,b2: a,b1,b2: . CoPrime(a,b1) . CoPrime(a,b1)   CoPrime(a,b2) CoPrime(a,b2)   CoPrime(a,b1 CoPrime(a,b1 b2) b2) | [coprime_prod] |
Thm*  a,b: a,b: . CoPrime(a,b) . CoPrime(a,b)   ( ( x,y: x,y: . a . a x+b x+b y = 1) y = 1) | [coprime_bezout_id] |
Thm*  a,b: a,b: . ( . ( x,y: x,y: . a . a x+b x+b y = 1) y = 1)   CoPrime(a,b) CoPrime(a,b) | [coprime_bezout_id2] |
Thm*  a,b: a,b: . CoPrime(a,b) . CoPrime(a,b)   ( ( x,y: x,y: . a . a x+b x+b y = 1) y = 1) | [coprime_bezout_id1] |
Thm*  a,b: a,b: . CoPrime(a,b) . CoPrime(a,b)   ( ( x,y: x,y: . (a . (a x+b x+b y) ~ 1) y) ~ 1) | [coprime_bezout_id0] |
Thm*  a,p: a,p: . prime(p) . prime(p)   (CoPrime(p,a) (CoPrime(p,a)    p | a) p | a) | [coprime_iff_ndivides] |
Thm*  a,b: a,b: . CoPrime(a,b) . CoPrime(a,b)   (gcd(a;b) ~ 1) (gcd(a;b) ~ 1) | [coprime_elim_a] |
Thm*  a,b: a,b: . CoPrime(a,b) . CoPrime(a,b)   ( ( c: c: . c | a . c | a   c | b c | b   (c ~ 1)) (c ~ 1)) | [coprime_elim] |
Thm*  a,b: a,b: . ( . ( c: c: . c | a . c | a   c | b c | b   c | 1) c | 1)   CoPrime(a,b) CoPrime(a,b) | [coprime_intro] |
Thm*  p: p: . prime(p) . prime(p)    p = 0 & p = 0 &  (p ~ 1) & ( (p ~ 1) & ( a: a: . a | p . a | p   (a ~ 1) (a ~ 1) 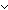 (a ~ p)) (a ~ p)) | [prime_elim] |
Thm*  a: a: . prime(a) . prime(a)   atomic(a) atomic(a) | [prime_imp_atomic] |
Thm*  a: a:  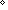 , b: , b: . a . a b | a b | a   (b ~ 1) (b ~ 1) | [self_divisor_mul] |
Thm*  a: a: . atomic(a) . atomic(a)    (a ~ 1) & ( (a ~ 1) & ( b: b: . b | a . b | a   (b ~ 1) (b ~ 1) 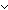 (b ~ a)) (b ~ a)) | [atomic_char] |
Thm*  i,j: i,j: . SqStable(CoPrime(i,j)) . SqStable(CoPrime(i,j)) | [sq_stable__coprime] |
Thm*  a,b,c: a,b,c: . gcd(gcd(a;b);c) ~ gcd(a;gcd(b;c)) . gcd(gcd(a;b);c) ~ gcd(a;gcd(b;c)) | [gcd_assoc] |
Thm*  a,b,n: a,b,n: . (n . (n gcd(a;b)) ~ gcd(n gcd(a;b)) ~ gcd(n a;n a;n b) b) | [gcd_mul] |
Thm*  a,b,y,n: a,b,y,n: . GCD(a;b;y) . GCD(a;b;y)   GCD(n GCD(n a;n a;n b;n b;n y) y) | [gcd_p_mul] |
Thm*  a,b: a,b: . .  u,v: u,v: . GCD(a;b;u . GCD(a;b;u a+v a+v b) b) | [bezout_ident] |
Thm*  b: b: , a: , a: . .  u,v: u,v: . GCD(a;b;u . GCD(a;b;u a+v a+v b) b) | [bezout_ident_n] |
Thm*  a,b: a,b: . .  y: y: . GCD(a;b;y) . GCD(a;b;y) | [gcd_exists] |
Thm*  b: b: , a: , a: . . 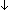  y: y: . GCD(a;b;y) . GCD(a;b;y) | [gcd_ex_n] |
Thm*  b: b: , a: , a: . .  y: y: . GCD(a;b;y) . GCD(a;b;y) | [gcd_exists_n] |
Thm*  a: a: , b: , b:  . .  q: q: , r: , r: b. a = q b. a = q b+r b+r | [quot_rem_exists] |
Thm*  a: a: , b: , b:  . .  q: q: , r: , r: b. a = q b. a = q b+r b+r | [quot_rem_exists_n] |
Thm*  a,b,c: a,b,c: . c | a . c | a   c | b c | b   c | gcd(a;b) c | gcd(a;b) | [gcd_is_gcd] |
Thm*  a,b: a,b: . gcd(a;b) | b . gcd(a;b) | b | [gcd_is_divisor_2] |
Thm*  a,b: a,b: . gcd(a;b) | a . gcd(a;b) | a | [gcd_is_divisor_1] |
Thm*  a,b: a,b: . gcd(a;b) ~ gcd(b;a) . gcd(a;b) ~ gcd(b;a) | [gcd_sym] |
Thm*  a,b: a,b: . .  y: y: . GCD(a;b;y) & gcd(a;b) = y . GCD(a;b;y) & gcd(a;b) = y | [gcd_elim] |
Thm*  a,b: a,b: . GCD(a;b;gcd(a;b)) . GCD(a;b;gcd(a;b)) | [gcd_sat_pred] |
Thm*  a,b: a,b: . GCD(a;b;gcd(a;b)) . GCD(a;b;gcd(a;b)) | [gcd_sat_gcd_p] |
Thm*  a,b: a,b: . gcd(a;b) . gcd(a;b) 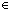  | [gcd_wf] |
Thm*  a,b,c,x,y: a,b,c,x,y: . .
Thm* GCD(a;b;x)
Thm*  
Thm* GCD(x;c;y)
Thm*  
Thm* y | a & y | b & y | c & ( z: z: . z | a . z | a   z | b z | b   z | c z | c   z | y) z | y) | [gcd_of_triple] |
Thm*  a,b,y1,y2: a,b,y1,y2: . GCD(a;b;y1) . GCD(a;b;y1)   GCD(a;b;y2) GCD(a;b;y2)   (y1 ~ y2) (y1 ~ y2) | [gcd_unique] |
Thm*  a,b,y,k: a,b,y,k: . GCD(a;b;y) . GCD(a;b;y)   GCD(a;b+k GCD(a;b+k a;y) a;y) | [gcd_p_shift] |
Thm*  a,b,y: a,b,y: . GCD(a;b;y) . GCD(a;b;y)   GCD(a;-b;y) GCD(a;-b;y) | [gcd_p_neg_arg_2] |
Thm*  a,b,y: a,b,y: . GCD(a;b;y) . GCD(a;b;y)   GCD(-a;b;y) GCD(-a;b;y) | [gcd_p_neg_arg_a] |
Thm*  a,b,y: a,b,y: . GCD(a;b;y) . GCD(a;b;y)   GCD(a;-b;y) GCD(a;-b;y) | [gcd_p_neg_arg] |
Thm*  a,b,y: a,b,y: . GCD(a;b;y) . GCD(a;b;y)   GCD(b;a;y) GCD(b;a;y) | [gcd_p_sym_a] |
Thm*  a,b,y: a,b,y: . GCD(a;b;y) . GCD(a;b;y)   GCD(b;a;y) GCD(b;a;y) | [gcd_p_sym] |
Thm*  a,b: a,b: . GCD(a;0;b) . GCD(a;0;b)   a = b a = b 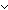 a = -b a = -b | [gcd_p_zero_rel] |
Thm*  a: a: . GCD(a;1;1) . GCD(a;1;1) | [gcd_p_one] |
Thm*  a: a: . GCD(a;0;a) . GCD(a;0;a) | [gcd_p_zero] |
Thm*  a: a: . GCD(a;a;a) . GCD(a;a;a) | [gcd_p_eq_args] |
Thm*  a,a',b,b',y,y': a,a',b,b',y,y': . .
Thm* (a ~ a')   (b ~ b') (b ~ b')   (y ~ y') (y ~ y')   (GCD(a;b;y) (GCD(a;b;y)   GCD(a';b';y')) GCD(a';b';y')) | [gcd_p_functionality_wrt_assoced] |
Thm*  a,b: a,b:  . a | b . a | b   ( ( c: c:  . b = a . b = a c c 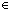   ) ) | [divides_nchar] |
Thm*  a: a: , b: , b:  . a | b & . a | b &  b | a b | a   a<b & a | b a<b & a | b | [pdivisor_bound] |
Thm*  a,b: a,b: . (a ~ b) . (a ~ b)   a = b a = b | [assoced_nelim] |
Thm*  a: a: . a | 1 . a | 1   (a ~ 1) (a ~ 1) | [unit_chars] |
Thm*  a: a: . |a| ~ a . |a| ~ a | [absval_assoced] |
Thm*  a: a: . (-a) ~ a . (-a) ~ a | [neg_assoced] |
Thm*  a,b: a,b: , n: , n:  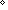 . ((n . ((n a) ~ (n a) ~ (n b)) b))   (a ~ b) (a ~ b) | [mul_cancel_in_assoced] |
Thm*  a,b: a,b: . (a ~ b) . (a ~ b)   a = b a = b 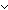 a = -b a = -b | [assoced_elim] |
Thm*  a,b,a',b': a,b,a',b': . (a ~ a') . (a ~ a')   (b ~ b') (b ~ b')   ((a ~ b) ((a ~ b)   (a' ~ b')) (a' ~ b')) | [assoced_functionality_wrt_assoced] |
Thm*  a,a',b,b': a,a',b,b': . (a ~ a') . (a ~ a')   (b ~ b') (b ~ b')   ((a ((a b) ~ (a' b) ~ (a' b')) b')) | [multiply_functionality_wrt_assoced] |
Thm*  a,b,c: a,b,c: . (a ~ b) . (a ~ b)   (b ~ c) (b ~ c)   (a ~ c) (a ~ c) | [assoced_transitivity] |
Thm*  a,b: a,b: . a = b . a = b   (a ~ b) (a ~ b) | [assoced_weakening] |
Thm*  a,a',b,b': a,a',b,b': . (a ~ a') . (a ~ a')   (b ~ b') (b ~ b')   (a | b (a | b   a' | b') a' | b') | [divides_functionality_wrt_assoced] |
Thm*  a,b: a,b: . Dec(a | b) . Dec(a | b) | [decidable__divides] |
Thm*  a: a: , n: , n:  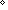 . n | a . n | a   (a (a 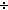 n) n) n = a n = a | [divides_iff_div_exact] |
Thm*  a: a: , b: , b:  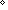 . b | a . b | a   (a rem b) = 0 (a rem b) = 0 | [divides_iff_rem_zero] |
Thm*  a: a: , b: , b:  . a | b . a | b   a a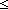 b b | [divisor_bound] |
Thm*  a,b: a,b: . a | b . a | b   ( ( n: n: . n . n a | n a | n b) b) | [divides_mul] |
Thm*  a,b,c: a,b,c: . a | b . a | b   a | b a | b c c | [divisor_of_mul] |
Thm*  a,b: a,b: . a | b . a | b   a | -b a | -b | [divisor_of_minus] |
Thm*  a,b1,b2: a,b1,b2: . a | b1 . a | b1   a | b2 a | b2   a | b1+b2 a | b1+b2 | [divisor_of_sum] |
Thm*  a,b: a,b: . a | b & b | a . a | b & b | a   a = a = 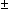 b b | [assoc_reln] |
Thm*  a,b: a,b: . a | b . a | b   b | a b | a   a = a = 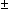 b b | [divides_anti_sym] |
Thm*  a,b: a,b: . a | b . a | b   b | a b | a   a = b a = b | [divides_anti_sym_n] |
Thm*  a,b,c: a,b,c: . a | b . a | b   b | c b | c   a | c a | c | [divides_transitivity] |
Thm*  a: a: . a | a . a | a | [divides_reflexivity] |
Thm*  a,b: a,b: . |a| | |b| . |a| | |b|   a | b a | b | [divides_of_absvals] |
Thm*  b: b: . b | 1 . b | 1   b = b = 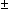 1 1 | [only_pm_one_divs_one] |
Thm*  a: a: , b: , b:  . a | b . a | b   a a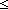 b b | [divisors_bound] |
Thm*  a,b: a,b: . a | b . a | b   a | -b a | -b | [divides_invar_2] |
Thm*  a,b: a,b: . a | b . a | b   -a | b -a | b | [divides_invar_1] |
Thm*  b: b: . b | 0 . b | 0 | [any_divs_zero] |
Thm*  a: a: . 1 | a . 1 | a | [one_divs_any] |
Thm*  a: a: . 0 | a . 0 | a   a = 0 a = 0 | [zero_divs_only_zero] |
Def prime(a) ==  a = 0 & a = 0 &  (a ~ 1) & ( (a ~ 1) & ( b,c: b,c: . a | b . a | b c c   a | b a | b 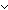 a | c) a | c) | [prime] |
Def GCD(a;b;y) == y | a & y | b & ( z: z: . z | a & z | b . z | a & z | b   z | y) z | y) | [gcd_p] |