| | Some definitions of interest. |
|
| assoced | Def a ~ b == a | b & b | a |
| | | Thm*  a,b: a,b: . (a ~ b) . (a ~ b) 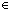 Prop Prop |
|
| gcd | Def gcd(a;b) == if b=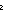 0 0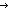 a else gcd(b;a rem b) fi (recursive) a else gcd(b;a rem b) fi (recursive) |
| | | Thm*  a,b: a,b: . gcd(a;b) . gcd(a;b) 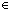  |
|
| gcd_p | Def GCD(a;b;y) == y | a & y | b & ( z: z: . z | a & z | b . z | a & z | b   z | y) z | y) |
| | | Thm*  a,b,y: a,b,y: . GCD(a;b;y) . GCD(a;b;y) 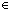 Prop Prop |