At: quotient of nsubn 2 1 2 1 1 2 1 1 2 1 1 2 1
1. n: {1+1...}
2.  E:(
E:( (n-1)
(n-1)

 (n-1)
(n-1)
 Prop).
(EquivRel x,y:
Prop).
(EquivRel x,y: (n-1). x E y) & (
(n-1). x E y) & ( x,y:
x,y: (n-1). Dec(x E y))
(n-1). Dec(x E y)) 
 (
(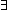 m:
m: (n-1+1).
(n-1+1).  m ~ (i,j:
m ~ (i,j: (n-1)//(i E j)))
(n-1)//(i E j)))
3. E:  n
n

 n
n
 Prop
Prop
4. EquivRel x,y: n. x E y
n. x E y
5.  x,y:
x,y: n. Dec(x E y)
n. Dec(x E y)
6. EquivRel x,y: (n-1). x E y
(n-1). x E y
7. m:  (n-1+1)
(n-1+1)
8. f:  m
m
 (i,j:
(i,j: (n-1)//(i E j))
(n-1)//(i E j))
9. g: (i,j: (n-1)//(i E j))
(n-1)//(i E j))

 m
m
10. InvFuns( m; i,j:
m; i,j: (n-1)//(i E j); f; g)
(n-1)//(i E j); f; g)
11.  x:
x: m. f(x)
m. f(x) 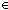 i,j:
i,j: n//(i E j)
n//(i E j)
12.  a:
a: n. a E a
n. a E a
13.  a,b:
a,b: n. (a E b)
n. (a E b) 
 (b E a)
(b E a)
14.  a,b,c:
a,b,c: n. (a E b)
n. (a E b) 
 (b E c)
(b E c) 
 (a E c)
(a E c)
15.  x,y:i,j:
x,y:i,j: n//(i E j). Dec(x = y)
n//(i E j). Dec(x = y)
16. Eb: (i,j: n//(i E j))
n//(i E j))
 (i,j:
(i,j: n//(i E j))
n//(i E j))

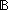
17.  x,y:i,j:
x,y:i,j: n//(i E j). (x Eb y)
n//(i E j). (x Eb y) 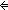
 x = y
x = y
18. 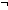 (
(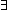 k:
k: (n-1). k E (n-1))
(n-1). k E (n-1))
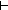 n-1
n-1 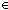 i,j:
i,j: n//(i E j)
n//(i E j)
By:
Assert (n-1 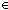
 n)
n)
THEN
Inclusion 19
Generated subgoals:None
About: