Step
*
1
2
1
1
1
of Lemma
FIM26_5
1. B : 





 @i'
@i'
2.  s,z,w:
s,z,w: . ((B s z)
. ((B s z) 
 (w
(w 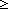 z )
z ) 
 (B s w))@i
(B s w))@i
3. b : 
4. 0 < b
5.  s:
s: . ((s
. ((s  b)
b) 
 (
( z:
z: . (B s z)))@i
. (B s z)))@i
6. z : 
7. B b z
8. z1 : 
9.  s:
s: . ((s
. ((s  (b - 1))
(b - 1)) 
 (B s z1))
(B s z1))

 z:
z: .
.  s:
s: . ((s
. ((s  b)
b) 
 (B s z))
(B s z))
BY
{ ((InstHyp [ b
b ;
; z
z ;
; imax(z1;z)
imax(z1;z) ] 2
] 2 THENA Auto) THEN Try ((Unfold `imax` 0 THEN AutoSplit))) }
THENA Auto) THEN Try ((Unfold `imax` 0 THEN AutoSplit))) }
1
1. B : 





 @i'
@i'
2.  s,z,w:
s,z,w: . ((B s z)
. ((B s z) 
 (w
(w 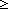 z )
z ) 
 (B s w))@i
(B s w))@i
3. b : 
4. 0 < b
5.  s:
s: . ((s
. ((s  b)
b) 
 (
( z:
z: . (B s z)))@i
. (B s z)))@i
6. z : 
7. B b z
8. z1 : 
9.  s:
s: . ((s
. ((s  (b - 1))
(b - 1)) 
 (B s z1))
(B s z1))
10. B b imax(z1;z)

 z:
z: .
.  s:
s: . ((s
. ((s  b)
b) 
 (B s z))
(B s z))
1. B : \mBbbN{} {}\mrightarrow{} \mBbbN{} {}\mrightarrow{} \mBbbP{}@i'
2. \mforall{}s,z,w:\mBbbN{}. ((B s z) {}\mRightarrow{} (w \mgeq{} z ) {}\mRightarrow{} (B s w))@i
3. b : \mBbbZ{}
4. 0 < b
5. \mforall{}s:\mBbbN{}. ((s \mleq{} b) {}\mRightarrow{} (\mexists{}z:\mBbbN{}. (B s z)))@i
6. z : \mBbbN{}
7. B b z
8. z1 : \mBbbN{}
9. \mforall{}s:\mBbbN{}. ((s \mleq{} (b - 1)) {}\mRightarrow{} (B s z1))
\mvdash{} \mexists{}z:\mBbbN{}. \mforall{}s:\mBbbN{}. ((s \mleq{} b) {}\mRightarrow{} (B s z))
By
((InstHyp [\mkleeneopen{}b\mkleeneclose{};\mkleeneopen{}z\mkleeneclose{};\mkleeneopen{}imax(z1;z)\mkleeneclose{}] 2\mcdot{} THENA Auto) THEN Try ((Unfold `imax` 0 THEN AutoSplit)))
Home
Index