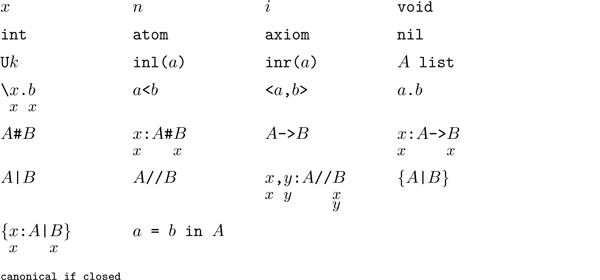The Book
Implementing Mathematics with The Nuprl Proof Development System
- Semantics
- The Type System in Detail
- The Rules
- The Form of a Rule
- Organization of the Rules
- Specifying a Rule
- Optional Parameters and Defaults
- Hidden Assumptions
- Shortcuts in the Presentation
- ATOM
- VOID
- INT
- LESS
- LIST
- UNION
- FUNCTION
- PRODUCT
- QUOTIENT
- SET
- EQUALITY
- UNIVERSE
- MISCELLANEOUS
- ML Constructors
- ATOM
- VOID
- INT
- LESS
- LIST
- UNION
- FUNCTION
- PRODUCT
- QUOTIENT
- SET
- EQUALITY
- UNIVERSE
- MISCELLANEOUS
The Rules
Semantics
The Nuprl semantics is a variation on that given by Martin-Löf for
his type theory [Martin-Löf 82]. There are three stages in the semantic specification:
the
computation system,
the type system and
the so-called judgement forms. Here
is how we shall proceed.
We shall specify a computation system consisting of terms,
divided
into canonical and
noncanonical, and a procedure for
evaluating
terms which for a given term ![]() returns at most one canonical term,
called the value of
returns at most one canonical term,
called the value of ![]() .
In Nuprl
whether a term is canonical depends only on the
outermost form of the term, and there are terms which
have no value.
We shall write
.
In Nuprl
whether a term is canonical depends only on the
outermost form of the term, and there are terms which
have no value.
We shall write
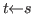 to mean that
to mean that ![]() has value
has value ![]() .
.
Next we shall specify a system of types. A type is a term ![]() (of the
computation system) with which is associated a transitive, symmetric
relation,
(of the
computation system) with which is associated a transitive, symmetric
relation, ![]() , which respects evaluation in
, which respects evaluation in ![]() and
and ![]() ;
that is, if
;
that is, if ![]() is a type and
is a type and
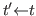 and
and
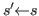 , then
, then ![]() if and only if
if and only if ![]() .
We shall sometimes say ``
.
We shall sometimes say ``![]() type'' to mean that
type'' to mean that ![]() is a type.
We say
is a type.
We say ![]() is a member of
is a member of ![]() , or
, or ![]() , if
, if ![]() .
Note that
.
Note that ![]() is an equivalence relation (in
is an equivalence relation (in ![]() and
and ![]() )
when restricted to members of
)
when restricted to members of ![]() .8.1Actually,
.8.1Actually, ![]() is a three-place relation on terms which respects evaluation
in all three places. We also use a transitive, symmetric relation on
terms,
is a three-place relation on terms which respects evaluation
in all three places. We also use a transitive, symmetric relation on
terms, ![]() , called type equality,
which
, called type equality,
which ![]() respects in
respects in ![]() ; that is,
if
; that is,
if ![]() then
then ![]() if and only if
if and only if ![]() .
The relation
.
The relation ![]() respects evaluation in
respects evaluation in ![]() and
and ![]() ,
and
,
and ![]() is a type if and only if
is a type if and only if ![]() .
The restriction of
.
The restriction of ![]() to types is an equivalence relation.
to types is an equivalence relation.
For our purposes, then, a type system for a given
computation system
consists of a two-place relation ![]() and a three-place relation
and a three-place relation ![]() on terms such that
on terms such that
We define ``is transitive and symmetric;
if and only if
&
;
is transitive and symmetric in
and
;
if and only if
&
;
if
;
if
&
.
type if and only if
;
if and only if
.
Finally, so-called judgements will be explained. This requires
consideration of terms with free variables
because substitution of closed
terms for free variables is central to judgements as presented
here.
In the description of semantics given so far
``term'' has meant a closed term, i.e., a term with no free variables.
There is only one form of judgement in Nuprl,
![]() :
:![]() ,
,![]() ,
,![]() :
:![]() »
» ![]() [ext
[ext ![]() ],
which in the case that
],
which in the case that ![]() is
is ![]() means
means ![]() .
The explanation of the cases in which
.
The explanation of the cases in which ![]() is not
is not ![]() must wait.
must wait.
Substitution
For the purposes of giving the procedure for evaluation and explaining the semantics of judgements, we would only need to consider substitution of closed terms for free variables and hence would not need to consider simultaneous substitution or capture. However, for the purpose of specifying inference rules later we shall want to have simultaneous substitution of terms with free variables for free variables. The result of such a substitution is indicated thus:where
The Computation System
Figure 8.1 shows the terms of Nuprl. Variables are terms, although since they are not closed they are not executable. Variables are written as identifiers, with distinct identifiers indicating distinct variables.8.2Nonnegative integers are written in standard decimal notation. There is no way to write a negative integer in Nuprl; the best one can do is to write a noncanonical term, such as -5, which evaluates to a negative integer. Atom constants are written as character strings enclosed in double quotes, with distinct strings indicating distinct atom constants.
The free occurrences of a variable ![]() in a term
in a term ![]() are the occurrences
of
are the occurrences
of ![]() which either are
which either are ![]() or are free in the immediate subterms of
or are free in the immediate subterms of ![]() ,
excepting those occurrences of
,
excepting those occurrences of ![]() which become bound
in
which become bound
in ![]() . In figure 8.1
the variables written below the terms indicate which variable
occurrences become bound; some examples are explained below.
. In figure 8.1
the variables written below the terms indicate which variable
occurrences become bound; some examples are explained below.
- In
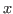 :
: #
#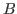 the
the 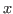 in front of the colon becomes bound
and any free occurrences of
in front of the colon becomes bound
and any free occurrences of 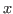 in
in 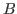 become bound.
The free occurrences of variables in
become bound.
The free occurrences of variables in 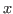 :
: #
#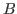 are
all the free occurrences of variables in
are
all the free occurrences of variables in  and
all the free occurrences of variables in
and
all the free occurrences of variables in 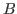 except for
except for 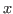 .
.
- In <
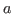 ,
,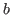 > no variable occurrences become bound; hence,
the free occurrences of variables in <
> no variable occurrences become bound; hence,
the free occurrences of variables in <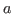 ,
,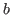 > are
those of
> are
those of 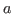 and those of
and those of 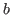 .
.
- In spread(
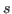 ;
;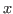 ,
,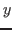 .
. ) the
) the 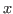 and
and 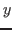 in front of the dot
and any free occurrences of
in front of the dot
and any free occurrences of 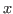 or
or 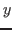 in
in  become bound.
become bound.
Parentheses may be used freely around terms and often must be used to resolve ambiguous notations correctly. Figure 8.2 gives the relative precedences and associativities of Nuprl operators.
The closed terms above the dotted line in figure 8.1 are the canonical terms, while the closed terms below it are the noncanonical terms. Note that carets appear below most of the noncanonical forms; these indicate the principal argument places of those terms. This notion is used in the evaluation procedure below. Certain terms are designated as redices, and each redex has a unique contractum. Figure 8.3 shows all redices and their contracta.
The evaluation procedure is as follows.
Given a (closed) term ![]() ,
,
- If
 is canonical then the procedure terminates with result
is canonical then the procedure terminates with result  .
.
- Otherwise, execute the evaluation procedure on each
principal argument of
 , and if each has a value,
replace the principal arguments of
, and if each has a value,
replace the principal arguments of  by their respective
values; call this term
by their respective
values; call this term 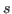 .
.
- If
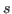 is a redex then the procedure for evaluating
is a redex then the procedure for evaluating  is continued
by evaluating the contractum of
is continued
by evaluating the contractum of 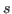 .
.
- If
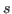 is not a redex then the procedure is terminated
without result;
is not a redex then the procedure is terminated
without result;  has no value.
has no value.
The Type System
For convenience we shall extend the relation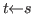 to possibly open terms.
If
to possibly open terms.
If 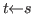 does not hold;
otherwise, it is true if and only if
does not hold;
otherwise, it is true if and only if 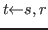 to mean that
to mean that
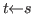 and
and
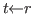 .
.
Recall that the members of a type are its canonical members and the
terms which have those members as values. The integers
are the canonical members of
the type int. The denumerably
many atom constants are the canonical members of the type atom.
The type void is empty. The type ![]() |
|![]() is like a disjoint
union of types
is like a disjoint
union of types ![]() and
and ![]() .
The terms inl(
.
The terms inl(![]() ) and inr(
) and inr(![]() ) are canonical members so long as
) are canonical members so long as
![]() and
and ![]() ;
; ![]() and
and ![]() need not be canonical.
(The operator names inl
and inr
are mnemonic for ``inject left'' and
``inject right''.) The canonical
members of
need not be canonical.
(The operator names inl
and inr
are mnemonic for ``inject left'' and
``inject right''.) The canonical
members of ![]() :
:![]() #
#![]() are the terms <
are the terms <![]() ,
,![]() > with
> with ![]() and
and ![]() ,
,
![]() and
and ![]() not necessarily canonical. Note that the type from which the
second component is selected may depend on the value of the first
component.
The canonical members of the type
not necessarily canonical. Note that the type from which the
second component is selected may depend on the value of the first
component.
The canonical members of the type ![]() list represent lists of members of
list represent lists of members of ![]() .
The empty list is represented by nil. A
nonempty list with head
.
The empty list is represented by nil. A
nonempty list with head ![]() is
represented by
is
represented by ![]() .
.![]() , where
, where ![]() evaluates to a member of the type
evaluates to a member of the type ![]() list
and represents the tail.
list
and represents the tail.
A term of the form ![]() (
(![]() ) is called an
application of
) is called an
application of ![]() to
to ![]() ,
and
,
and ![]() is called its argument.
The members of
is called its argument.
The members of ![]() :
:![]() ->
->![]() are called functions,
and each
canonical member is a lambda term,
are called functions,
and each
canonical member is a lambda term,
\![]() .
.![]() ,
whose application to any
,
whose application to any ![]() is a member of
is a member of ![]() .
It is required that applications to equal members of type
.
It is required that applications to equal members of type ![]() be equal.
Clearly,
be equal.
Clearly, ![]() (
(![]() )
)![]() if
if ![]()
![]() :
:![]() ->
->![]() and
and ![]() .
.
The significance of some constructors derives from the representation
of propositions as types.
A proposition represented by a type is true if and only if the type
is inhabited. The type ![]() <
<![]() is inhabited
if and only if the value of
is inhabited
if and only if the value of ![]() is less than the value of
is less than the value of ![]() .
The type (
.
The type (![]() =
=![]() in
in ![]() ) is inhabited if and only if
) is inhabited if and only if ![]() .
Obviously, the type (
.
Obviously, the type (![]() =
=![]() in
in ![]() ) is inhabited if and only if
) is inhabited if and only if ![]() ,
so ``
,
so ``![]() in
in ![]() '' has been adopted as a notation for this type.
The members of {
'' has been adopted as a notation for this type.
The members of {![]() :
:![]() |
|![]() } are the
members
} are the
members ![]() of
of ![]() such that
such that ![]() is inhabited.
Types of the form {
is inhabited.
Types of the form {![]() :
:![]() |
|![]() } are called
set types.
The set constructor provides a device for specifying subtypes;
for example, {x:int|0<x} has just the positive integers
as canonical members.
} are called
set types.
The set constructor provides a device for specifying subtypes;
for example, {x:int|0<x} has just the positive integers
as canonical members.
The members of ![]() ,
,![]() :
:![]() //
//![]() are the members of
are the members of ![]() .
The difference between this type and
.
The difference between this type and ![]() is equality.
is equality.
![]()
![]() ,
,![]() :
:![]() //
//![]() if and only if
if and only if ![]() and
and ![]() are members
of
are members
of ![]() and
and ![]() is inhabited.
Types of this form are called quotient types.
The relation
is inhabited.
Types of this form are called quotient types.
The relation
![]() is an equivalence relation
over
is an equivalence relation
over ![]() in
in ![]() and
and ![]() ;
this is built into the criteria for
;
this is built into the criteria for ![]() ,
,![]() :
:![]() //
//![]() being a type.
being a type.
Now consider equality on the other types already discussed.
(Recall that
terms are equal in a given type if and only if they evaluate to canonical
terms equal in that type.
Recall also that ![]() is an equivalence relation
in
is an equivalence relation
in ![]() and
and ![]() when restricted to members of
when restricted to members of ![]() .)
Members of int are equal
(in int) if and only if they have the same value.
The same goes for type atom.
Canonical members of
.)
Members of int are equal
(in int) if and only if they have the same value.
The same goes for type atom.
Canonical members of ![]() |
|![]() (
(![]() :
:![]() #
#![]() ,
, ![]() list) are
equal if and only if they have the same outermost operator and their
corresponding immediate subterms are equal (in the corresponding types).
Members of
list) are
equal if and only if they have the same outermost operator and their
corresponding immediate subterms are equal (in the corresponding types).
Members of ![]() :
:![]() ->
->![]() are equal if and only if their applications
to any member
are equal if and only if their applications
to any member ![]() of
of ![]() are equal in
are equal in ![]() .
We say equality on
.
We say equality on ![]() :
:![]() ->
->![]() is extensional.
The types
is extensional.
The types ![]() <
<![]() and (
and (![]() =
=![]() in
in ![]() ) have
at most one canonical member, axiom.
Equality in {
) have
at most one canonical member, axiom.
Equality in {![]() :
:![]() |
|![]() } is just the
restriction of equality in
} is just the
restriction of equality in ![]() to {
to {![]() :
:![]() |
|![]() }.
}.
We must now consider the notion of functionality.
A term ![]() is type-functional in
is type-functional in ![]() if and only if
if and only if
![]() is a type and
is a type and
![]() for any
for any ![]() and
and ![]() such that
such that ![]() .
A term
.
A term ![]() is
is ![]() -functional in
-functional in ![]() if and only if
if and only if
![]() is type-functional in
is type-functional in ![]() and
and
![]() for any
for any ![]() and
and ![]() such that
such that
![]() .
There are restrictions on type formation involving type-functionality.
These can be seen in the type formation clauses
of section 8.2 for
.
There are restrictions on type formation involving type-functionality.
These can be seen in the type formation clauses
of section 8.2 for ![]() :
:![]() #
#![]() ,
,
![]() :
:![]() ->
->![]() , and {
, and {![]() :
:![]() |
|![]() }.
In each of these
}.
In each of these ![]() must be type-functional in
must be type-functional in ![]() :
:![]() .8.3We may now say that the members of
.8.3We may now say that the members of ![]() :
:![]() ->
->![]() are the lambda terms
are the lambda terms
\![]() .
.![]() such that
such that ![]() is
is ![]() -functional in
-functional in ![]() .
In the type
.
In the type ![]() ,
,![]() :
:![]() //
//![]() , that
, that ![]() must be type-functional in both
must be type-functional in both
![]() ,
,![]() :
:![]() follows
from the fact that
follows
from the fact that ![]() :
:![]() ->
->![]() :
:![]() ->
->![]() ->
->![]() must be a type.
There are also constraints on the typehood of
must be a type.
There are also constraints on the typehood of ![]() ,
,![]() :
:![]() //
//![]() which
guarantee that the relation
which
guarantee that the relation
![]() is an equivalence relation on members
of
is an equivalence relation on members
of ![]() and respects equality in
and respects equality in ![]() .
It should be noted that if
.
It should be noted that if ![]() is empty then every term is type-functional
in its free variables over
is empty then every term is type-functional
in its free variables over ![]() . Hence,
. Hence, ![]() :void#3 is a type
(with no members) even though 3 is not a type.
:void#3 is a type
(with no members) even though 3 is not a type.
Equal types have the same membership and equality, but not conversely.
Type equality in
Nuprl is not extensional;
that is, it is not enough for type equality that two types should have
the same membership and equality. In Nuprl equal canonical types always
have the same outermost type constructor.8.4The relations that must hold between the
respective immediate subterms are seen easily enough in the definition of type
equality given in section 8.2 on page ![]() .
It should be noted that in contrast to equality between types of the form
.
It should be noted that in contrast to equality between types of the form
![]() :
:![]() #
#![]() or
or ![]() :
:![]() ->
->![]() ,
much less is required for
{
,
much less is required for
{![]() :
:![]() |
|![]() }
}![]() {
{![]() :
:![]() |
|![]() } than type-functional
equality of
} than type-functional
equality of ![]() and
and ![]() in
in ![]() :
:![]() . All that is required is the existence
of functions which for each
. All that is required is the existence
of functions which for each ![]() evaluate to functions
mapping back and forth between
evaluate to functions
mapping back and forth between ![]() and
and ![]() .
Equality between quotient types is defined similarly.
If
.
Equality between quotient types is defined similarly.
If ![]() does not occur free in
does not occur free in ![]() then
then ![]() #
#![]()
![]()
![]() :
:![]() #
#![]() ,
,
![]() ->
->![]()
![]()
![]() :
:![]() ->
->![]() ,
and {
,
and {![]() |
|![]() }
}![]() {
{![]() :
:![]() |
|![]() };
if
};
if ![]() and
and ![]() do not occur free in
do not occur free in ![]() then
then
![]() //
//![]()
![]()
![]() ,
,![]() :
:![]() //
//![]() .
As a result there is no need for clauses in the type system description
giving the criteria for
.
As a result there is no need for clauses in the type system description
giving the criteria for ![]()
![]() #
#![]() and the others explicitly.
and the others explicitly.
Now consider the so-called universes,
![]() (
(![]() positive).
The members of
positive).
The members of ![]() are types. The universes are
cumulative; that is,
if
are types. The universes are
cumulative; that is,
if ![]() is less than
is less than ![]() then membership and equality in
then membership and equality in ![]() are just
restrictions of membership and equality in
are just
restrictions of membership and equality in ![]() .
Universe
.
Universe ![]() is closed
under all the type-forming operations except formation
of
is closed
under all the type-forming operations except formation
of ![]() for
for ![]() greater than or equal to
greater than or equal to ![]() .
Equality (hence membership) in
.
Equality (hence membership) in ![]() is similar to
type equality as defined previously
except that equality (membership) in
is similar to
type equality as defined previously
except that equality (membership) in ![]() is
required wherever type equality (typehood) was formerly required,
and although all universes are types, only those U
is
required wherever type equality (typehood) was formerly required,
and although all universes are types, only those U![]() such that
such that ![]() is less
than
is less
than ![]() are in
are in ![]() . Equality in
. Equality in ![]() is the restriction
of type equality to members of
is the restriction
of type equality to members of ![]() .
.
So far the only noncanonical form explicitly
mentioned in
connection with the type system is application. We shall elaborate
here on a couple of forms, and it should then be easy to
see how to treat the others. The spread form is
used for computational
analysis of pairs. The pair of components is spread apart
so that the components can be used separately.
spread(![]() ;
;![]() ,
,![]() .
.![]() )
)![]() if
if
![]()
& ![]() is type functional in
is type functional in ![]() :(
:(![]() :
:![]() #
#![]() )
)
&
![]() <
<![]() ,
,![]() >
>![]()
if ![]() and
and ![]()
Since
![]() then for some
then for some ![]() and
and ![]()
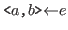 where
where ![]() , and
, and ![]() .
Hence
.
Hence
![]() and
and
![]() have the same value, so it is enough
that
have the same value, so it is enough
that
![]() But from our hypotheses it follows that
But from our hypotheses it follows that
![]() so it is enough that
so it is enough that
![]() Now
Now
![]() since
since ![]()
![]() :
:![]() #
#![]() and equality respects evaluation;
therefore
and equality respects evaluation;
therefore
![]() in light of
in light of
![]() 's functionality in
's functionality in ![]() :(
:(![]() :
:![]() #
#![]() ).8.5
).8.5
The list induction form allows one to perform
inductive
analysis of lists.
list_ind(![]() ;
;![]() ;
;![]() ,
,![]() .
.![]() ) is a function (in
) is a function (in ![]() ) which
halts on all members of
) which
halts on all members of ![]() list. It is the function (in
list. It is the function (in ![]() ) defined by primitive
recursion,
where
) defined by primitive
recursion,
where ![]() is the result for the base case of
is the result for the base case of ![]() nil (in
nil (in ![]() list) and
list) and
![]() shows how to build the value for
shows how to build the value for ![]()
![]() .
.![]() (in
(in ![]() list) from
list) from ![]() ,
, ![]() and the value
of the function being defined on
and the value
of the function being defined on ![]() , this value being passed through
, this value being passed through ![]() during
evaluation.
during
evaluation.
![]() if
if
![]()
![]() list
list
& ![]() is type functional in
is type functional in ![]() :(
:(![]() list)
list)
& ![]() nil
nil![]()
&
![]()
if ![]() &
&
![]() &
& ![]()
Let us prove this by induction on the length of the list
represented by ![]() , all other variables universally quantified.
Suppose
, all other variables universally quantified.
Suppose
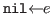 . By definition we know that
list_ind(
. By definition we know that
list_ind(![]() ;
;![]() ;
;![]() ,
,![]() ,
,![]() .
.![]() )
and
)
and ![]() have the same value,
so it is enough for the base case that
have the same value,
so it is enough for the base case that ![]() ;
this is true since
;
this is true since ![]() is functional in
is functional in ![]()
![]() list,
list,
![]() , and
, and
![]() .
Now suppose that for some
.
Now suppose that for some ![]() and
and ![]() ,
, ![]() .
.![]()
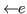 ,
, ![]() , and
, and
![]() .
Now
.
Now
and
have the same value, so it is enough that the substitution into
It follows that the substitution into
The decide form is used to discern a left from a right injection, and to permit computation on the injected term. The ind form is used to define functions recursively on integers.8.6The reader is referred to chapter 2 or to the exposition of the rules for further elaboration of the use of noncanonical forms.
Judgements
The significance of the so-called judgements lies in the fact that they constitute the claims of a Nuprl proof. They are the units of assertion; they are the objects of inference. The judgements of Nuprl have the formwhere
Before explaining the conditions which make a Nuprl sequent true
we shall define a relation ![]() , where
, where ![]() is a hypothesis list and
is a hypothesis list and
![]() is a list of terms,
and we shall define what it is for a sequent to be true at
a list of terms.
is a list of terms,
and we shall define what it is for a sequent to be true at
a list of terms.
![]() :
:![]() ,
,![]() ,
,![]() :
:![]()
![]()
![]() if and only if
if and only if
![]()
&
![\( \forall t_1',\dots,t_j'.\,\, T_{j+1}[t_1,\dots,t_j/x_1,\dots,x_j]=\\ *
\hspace*{1em}\hspace*{4em}\hspace*{4em} T_{j+1}[t_1',\dots,t_j'/x_1,\dots,x_j] \)](img581.png)
if
![]()
We can also express this relation by saying that
every ![]() is a member of
is a member of
and every
The sequent
is true at
&
if
&
Equivalently, we can say that
The connection between functionality and the truth of sequents lies in the fact that
It is not always necessary to declare a variable with every hypothesis in a hypothesis list. If a declared variable does not occur free in the conclusion, extract term or any hypothesis, then the variable (and the colon following it) may be omitted.
In Nuprl it is not possible for the user to enter a complete
sequent directly; the extract term must be omitted.
In fact, a sequent is never displayed with its extract term.
The system has been designed so that upon completion of a proof,
the system automatically provides, or extracts, the extract term.
This is because in what is anticipated to be the standard mode of use,
the user tries to prove that a certain type is inhabited without
regard to the identity of any member.
One expects that in this mode the user thinks of the type
(that is to be shown inhabited) as a proposition, and that it
is merely the truth of this proposition that the user wants to show.
When one does wish to show explicitly that ![]() or that
or that ![]() ,
one instead shows the type (
,
one instead shows the type (![]() =
= ![]() in
in ![]() ) or the type
(
) or the type
(![]() in
in ![]() ) to be inhabited.8.8
) to be inhabited.8.8
Also, the system can often extract a term from an incomplete proof when the extraction is independent of the extract terms of any unproven claims within the proof body. Of course, such unproven claims may still contribute to the truth of the proof's main claim. For example, it is possible to provide an incomplete proof of the untrue sequent » 1<1 [ext axiom], the extract term axiom being provided automatically.
Although the term extracted from a proof of a sequent is not displayed in the sequent, the term is accessible by other means through the name assigned to the proof in the user's library. It should be noted that in the current system proofs named in the user's library cannot be proofs of sequents with hypotheses.
The Type System in Detail
This section may be skipped on the first reading, as the informal description of the type system given in section 8.1 should meet the needs of most readers.This section consists of two parts. First, we give the formal definition of Nuprl's type system by means of a recursive definition of the necessary predicates. Then, for ease of understanding and reference, from the definition we extract criteria for typehood and membership. Those who do read this section may benefit by reading the latter part first.
Formal Definition of Equality
What follows is a recursive definition of four predicates--
![]() range over possibly open terms,
range over possibly open terms,
![]() range over variables;
range over variables;
![]() range over positive integers;
range over positive integers;
![]() range over integers;
range over integers;
![]() ranges over atom constants.
ranges over atom constants.
![]() type iff
type iff ![]()
![]() iff
iff ![]()
![]() iff void
iff void
 or atom
or atom
 or int
or int
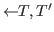
or
![]() (
(![]() =
=![]() in
in ![]() )
)
 & (
& (![]() =
=![]() in
in ![]() )
)

& ![]() &
& ![]() &
& ![]()
or
![]() (
(![]() <
<![]() )
)
 & (
& (![]() <
<![]() )
)
 &
& ![]() int &
int & ![]() int
int
or
![]()
![]() list
list
 &
& ![]() list
list
 &
& ![]()
or
![]()
![]() |
|![]()
 &
& ![]() |
|![]()
 &
& ![]() &
& ![]()
or
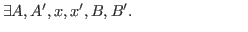 (
( ![]() :
:![]() #
#![]()
 or
or ![]() #
#![]()
 )
)
& ( ![]() :
:![]() #
#![]()
 or
or ![]() #
#![]()
 )
)
& ![]() &
&
![]() if
if ![]()
or
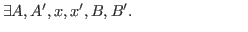 (
( ![]() :
:![]() ->
->![]()
 or
or ![]() ->
->![]()
 )
)
& ( ![]() :
:![]() ->
->![]()
 or
or ![]() ->
->![]()
 )
)
& ![]() &
&
![]() if
if ![]()
or
![]()
( {![]() :
:![]() |
|![]() }
}
 or {
or {![]() |
|![]() }
}
 )
)
& ( {![]() :
:![]() |
|![]() }
}
 or {
or {![]() |
|![]() }
}
 )
)
& ![]() &
& ![]() occurs in neither
occurs in neither ![]() nor
nor ![]()
& ![]()
![]() :
:![]() ->
->![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]() ->
->![]()
or
![]()
( ![]() ,
,![]() :
:![]() //
//![]()
 or
or ![]() //
//![]()
 )
)
& ( ![]() ,
,![]() :
:![]() //
//![]()
 or
or ![]() //
//![]()
 )
)
& ![]()
& ![]() are distinct and occur in neither
are distinct and occur in neither ![]() nor
nor ![]()
& ![]()
![]() :
:![]() ->
->![]() :
:![]() ->
->![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]() :
:![]() ->
->![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]() :
:![]() ->
->![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]() :
:![]() ->
->![]() :
:![]() ->
->![]() ->
->![]() ->
->
![]()
or
![]() U
U![]()
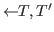
![]() if
if ![]() &
& ![]()
not ![]() void
void
![]() atom iff
atom iff
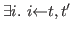
![]() int iff
int iff
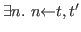
![]() (
(![]() =
=![]() in
in ![]() ) iff axiom
) iff axiom
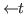 &
& ![]()
![]()
![]() <
<![]() iff axiom
iff axiom
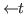 &
&
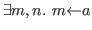 &
&
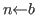 &
& ![]() is less than
is less than ![]()
![]()
![]() list iff
list iff ![]() list type
list type
& nil
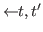 or
or
![]() (
(![]() .
.![]() )
)
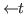 & (
& (![]() .
.![]() )
)
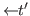
& ![]() &
& ![]()
![]() list
list
![]()
![]() |
|![]() iff
iff ![]() |
|![]() type
type
& (
![]() inl(
inl(![]() )
)
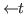 & inl(
& inl(![]() )
)
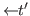 &
& ![]() )
)
or
![]() inr(
inr(![]() )
)
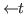 & inr(
& inr(![]() )
)
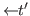 &
& ![]()
![]()
![]() :
:![]() #
#![]() iff
iff ![]() :
:![]() #
#![]() type
type
&
![]() <
<![]() ,
,![]() >
>
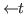 & <
& <![]() ,
,![]() >
>
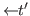
& ![]() &
&
![]()
![]()
![]() :
:![]() ->
->![]() iff
iff ![]() :
:![]() ->
->![]() type
type
&
![]()
\![]() .
.![]()
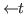 &
& \![]() .
.![]()
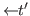
&
![]()
if ![]()
![]() {
{![]() :
:![]() |
|![]() } iff {
} iff {![]() :
:![]() |
|![]() } type &
} type & ![]() &
&
![]()
![]()
![]() ,
,![]() :
:![]() //
//![]() iff
iff ![]() ,
,![]() :
:![]() //
//![]() type &
type & ![]() &
& ![]()
&
![]()
![]() U
U![]() iff void
iff void
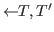 or atom
or atom
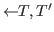 or int
or int
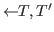
or
![]() (
(![]() =
=![]() in
in ![]() )
)
 & (
& (![]() =
=![]() in
in ![]() )
)

& ![]() U
U![]() &
& ![]() &
& ![]()
or
![]() (
(![]() <
<![]() )
)
 & (
& (![]() <
<![]() )
)

& ![]() int &
int & ![]() int
int
or
![]()
![]() list
list
 &
& ![]() list
list
 &
& ![]() U
U![]()
or
![]()
![]() |
|![]()
 &
& ![]() |
|![]()

& ![]() U
U![]() &
& ![]() U
U![]()
or
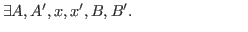 (
( ![]() :
:![]() #
#![]()
 or
or ![]() #
#![]()
 )
)
& ( ![]() :
:![]() #
#![]()
 or
or ![]() #
#![]()
 )
)
& ![]() U
U![]()
&
![]() U
U![]() if
if ![]()
or
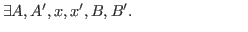 (
( ![]() :
:![]() ->
->![]()
 or
or ![]() ->
->![]()
 )
)
& ( ![]() :
:![]() ->
->![]()
 or
or ![]() ->
->![]()
 )
)
& ![]() U
U![]()
&
![]() U
U![]() if
if ![]()
or
![]()
( {![]() :
:![]() |
|![]() }
}
 or {
or {![]() |
|![]() }
}
 )
)
& ( {![]() :
:![]() |
|![]() }
}
 or {
or {![]() |
|![]() }
}
 )
)
& ![]() U
U![]()
&
![]() U
U![]() if
if ![]()
&
![]() U
U![]() if
if ![]()
& ![]() occurs in neither
occurs in neither ![]() nor
nor ![]()
& ![]()
![]() :
:![]() ->
->![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]() ->
->![]()
or
![]()
( ![]() ,
,![]() :
:![]() //
//![]()
 or
or ![]() //
//![]()
 )
)
& ( ![]() ,
,![]() :
:![]() //
//![]()
 or
or ![]() //
//![]()
 )
)
& ![]() U
U![]()
&
![]() U
U![]() if
if ![]() &
& ![]()
&
![]() U
U![]() if
if ![]() &
& ![]()
& ![]() are distinct and occur in neither
are distinct and occur in neither ![]() nor
nor ![]()
& ![]()
![]() :
:![]() ->
->![]() :
:![]() ->
->![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]() :
:![]() ->
->![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]() :
:![]() ->
->![]() ->
->![]()
& ![]()
![]() :
:![]() ->
->![]() :
:![]() ->
->![]() :
:![]() ->
->![]() ->
->![]() ->
->
![]()
or
![]() U
U![]()
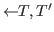 &
& ![]() is less than
is less than ![]()
Typehood and Membership
What follows is not a definition but a body of facts easily derived from the definition above. or atom
or atom
 or int
or int

or
 &
& or
 &
& or
 &
& or
 &
& or
 or
or  )
)
&
or
 or
or  )
)
&
or
 or {
or { )
)
&
or
(
 or
or  )
)
&
&
&
&
&
or

not
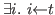
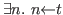
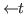 &
& 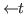 &
&
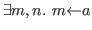 &
&
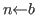 &
& & nil
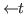 or
or
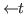 &
& & (
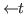 &
& 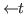 &
& 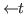 &
& &
\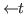
&
if
 or atom
or atom
 or int
or int

or
 &
& or
 &
& or
 &
& or
 &
& or
 or
or  )
)
&
or
 or
or  )
)
&
or
 or {
or { )
)
&
or
(
 or
or  )
)
&
&
if
&
&
&
&
or
 &
& The Rules
The Nuprl system has been designed to accommodate the top-down construction of proofs by refinement. In this style one proves a judgement (i.e., a goal) by applying a refinement rule, thereby obtaining a set of judgements called subgoals, and then proving each of the subgoals. The mechanics of using the proof-editing system were discussed in chapter 7. In this section we will describe the refinement rules themselves. First we give some general comments regarding the rules and then proceed to give a description of each rule.
The Form of a Rule
To accommodate the top-down style of the Nuprl system the rules of the logic are presented in the following refinement style.The goal is shown at the top, and each subgoal is shown indented underneath. The rules are defined so that if every subgoal is true then one can show the truth of the goal, where the truth of a judgement is to be understood as defined in section 8.1. If there are no subgoals (
One of the features of the proof editor is that
the extraction terms are not
displayed and indeed are not immediately available.
The idea is that one can judge a term ![]() to be a type and
to be a type and ![]() to be
inhabited without explicitly presenting the inhabiting object.
When one is viewing
to be
inhabited without explicitly presenting the inhabiting object.
When one is viewing ![]() as a proposition this is convenient, as a
proposition is true if it is inhabited.
If
as a proposition this is convenient, as a
proposition is true if it is inhabited.
If ![]() is being viewed as a specification this allows one to
implicitly
build a program which is guaranteed to be correct for the specification.
The extraction term for a goal is built as a function of the extraction
terms of the subgoals and thus in general cannot be built until each of
the subgoals have been proved.
If one has a specific term,
is being viewed as a specification this allows one to
implicitly
build a program which is guaranteed to be correct for the specification.
The extraction term for a goal is built as a function of the extraction
terms of the subgoals and thus in general cannot be built until each of
the subgoals have been proved.
If one has a specific term, ![]() , in mind as the inhabiting object and wants
it displayed, one can use the explicit intro rule and then show that the
type
, in mind as the inhabiting object and wants
it displayed, one can use the explicit intro rule and then show that the
type ![]() in
in ![]() is inhabited.
The rules have the property that each subgoal can be constructed from the
information in the rule and from the goal, exclusive of the extraction term.
As a result some of the more complicated rules require certain terms as
parameters.
is inhabited.
The rules have the property that each subgoal can be constructed from the
information in the rule and from the goal, exclusive of the extraction term.
As a result some of the more complicated rules require certain terms as
parameters.
Implicit in showing a judgement to be true is showing that the conclusion of
the judgement is in fact a type.
We cannot directly judge a term to be a type; rather, we show that it
inhabits a universe.
An examination of the semantic definition will reveal that this is
sufficient for our purposes.
Due to the rich type structure of the system it is not possible in general
to decide algorithmically if a given term denotes an element of a universe,
so this is something which will require proof.
The logic has been arranged so the proof that the conclusion of a goal
is a type can be conducted simultaneously with the proof that the type is
inhabited.
In many cases this causes no great overhead,
but some rules have subgoals whose only purpose is to establish that the
goal is a type, that is, that it is well-formed.
These subgoals all have the form ![]() »
» ![]() in
in  and are referred
to as well-formedness subgoals.
and are referred
to as well-formedness subgoals.
Organization of the Rules
The rules for reasoning about each type and objects of the type will be presented in separate sections. Recall from above that for each judgement of the form- Formation
These rules give the conditions under which a canonical type may be judged to inhabit a universe, thus verifying that it is indeed a type. - Canonical
These rules give the conditions under which a canonical object (implicitly or explicitly presented) may be judged to inhabit a canonical type. Note that the formation rules are all actually canonical rules, but it is convenient to separate them. - Noncanonical
These rules give the conditions under which a noncanonical object may be judged to inhabit a type. The elimination rules all fall in this category, as the extract term for an elimination rule is a noncanonical term. - Equality
These rules give the conditions under which objects having the same outer form may be judged to be equal. Recall that the rules are being presented in implicit/explicit pairs,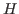 »
» 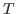 ext
ext  and
and 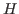 »
»  in
in 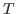 .
The explicit judgement
.
The explicit judgement 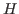 »
»  in
in 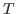 is simply
the reflexive instance of the general equality judgement
is simply
the reflexive instance of the general equality judgement
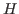 »
»  =
= 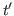 in
in 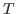 , and in most cases the rule for the
general form is an obvious generalization of the rule for the reflexive
form, and thus will be omitted.
As the rules for the reflexive judgement are given in one of the other
categories, there will be no equality rules presented for some types.
, and in most cases the rule for the
general form is an obvious generalization of the rule for the reflexive
form, and thus will be omitted.
As the rules for the reflexive judgement are given in one of the other
categories, there will be no equality rules presented for some types.
- Computation
These rules allow one to make judgements of equalities resulting from computation.
Rules such as the sequence, hypothesis and lemma rules which are not associated with one particular type are grouped together under the heading "miscellaneous".
Specifying a Rule
In the context of a particular goal a rule is specified by giving a name and, possibly, certain parameters. As there are a large number of rules it would be unfortunate to have to remember a unique name for each one. Instead, there are small number of generic names, and the proof editor infers the specific rule desired from the form of the goal. In fact, for the rules dealing with specific types or objects of specific types, there are only the names intro, elim and reduce. The intro rules are those which break down the conclusion of the goal, and the elim rules are those which use a hypothesis. Accordingly, the first parameter of any elim rule is the declared variable or number of the hypothesis to be used. The reduce rules are the computation rules. The first parameter of a reduce rule is a number that specifies which term of the equality is to be reduced. Among the parameters of some rules are keyword parameters which have the following form:- new
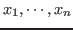
This parameter is used to give new names for hypotheses in the subgoals. In most cases the defaults, which are derived from subterms of the conclusion of the goal, suffice. For technical reasons the same variable can be declared at most once in a hypothesis list, so if a default name is already declared a new name will have to be given. Whenever this parameter is used it must be the case that the names given are all distinct and do not occur in the hypothesis list of the goal. - using
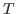 , over
, over 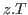
These parameters are used when judging the equality of noncanonical forms in types dependent on the principal argument of the noncanonical form. The using parameter specifies the type of the principal argument of the noncanonical form. The value should be a canonical type which is appropriate for the particular noncanonical form. The over parameter specifies the dependence of the type over which the equality is being judged on the principal argument of the form. Each occurrence of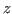 in
in 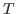 indicates such a dependency.
The proof editor always checks that the term obtained by substituting the
principal argument for
indicates such a dependency.
The proof editor always checks that the term obtained by substituting the
principal argument for 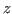 in
in 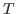 is
is
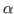 -convertible
to the type of the equality judgement.
-convertible
to the type of the equality judgement.
- at
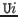
The value of this parameter is the universe level at which any type judgements in the subgoals are to be made. The default is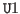 .
.
Optional Parameters and Defaults
Each rule will be presented in its most general form. However, some of the parameters of a rule may be optional, in which case they will be enclosed by square brackets ([]). If a new hypothesis in a subgoal depends on an optional parameter, and in a particular instance of the rule the optional parameter is not given, that new hypothesis will not be added. Such a dependence is usually in the form of a hypothesis specifically referring to an optional new name. The over parameter discussed above is almost always optional. If it is not given, it is assumed that the type of the equality has no dependence on the principal argument of the noncanonical form.The issue of default values for variable names arises when the main term of a goal's conclusion contains binding variables. In general, the default values are taken to be those binding variables. For example, the rule for explicitly showing a product to be in a universe is
![]() »
» ![]() :
:![]() #
#![]() in
in  by intro [new y]
by intro [new y]
» ![]() in
in 
![]() :
:![]() »
» ![]() in
in 
The rule is presented as if a new name is given, but the default is to
use ![]() .
All the dependent types follow this general pattern.
.
All the dependent types follow this general pattern.
For judging the equality of terms containing binding variables the binding variables of the first term are in general the default values for the ``appropriate'' new hypotheses. Consider the rule for showing that a spread term is in a type:
![]() » spread(
» spread(![]() ;
;![]() ) in
) in ![]() [
[![]() /
/![]() ]
]
by intro [over ![]() ] using
] using ![]() :
:![]() #
#![]() [new
[new ![]() ]
]
![]() »
» ![]() in
in ![]() :
:![]() #
#![]()
![]() ,
,![]() :
:![]() ,
,![]() :
:![]() [
[![]() /
/![]() ] »
] »
![]() [
[![]() /
/![]() ] in
] in ![]() [<
[<![]() ,
,![]() >/
>/![]() ]
]
Here the new variables default to ![]() . If no new names are given and
. If no new names are given and
![]() and
and ![]() don't appear in
don't appear in ![]() , then the second subgoal will be
, then the second subgoal will be
![]() ,
,![]() :
:![]() ,
,![]() :
:![]() »
» ![]() in
in ![]() [<
[<![]() ,
,![]() >/
>/![]() ]
]
Again this is the general pattern for rules of this type.
Hidden Assumptions
For certain rules, we need to be able to control the free variables occuring in the extract term. The mechanism used to achieve this is that of hidden hypotheses. A hypothesis is hidden when it is displayed enclosed in square brackets. At the moment the only place where such hypotheses are added is in a subgoal of the set elim rule. The intended meaning of a hypothesis being hidden is that the name of the hypothesis cannot appear free in the extracted term; that is, that it cannot be used computationally. Accordingly, a hidden hypothesis cannot be the object of an elim or hyp rule. For the rules for which the extract term is the trivial term axiom, the extract term contains no free variable references and so all restrictions on the use of hidden hypotheses can be removed. The editor will remove the brackets from any hidden hypotheses in displaying a goal of this form.Shortcuts in the Presentation
With the exception of one of the direct computation rules, each of the rules has the property that the list of hypotheses in a subgoal is an extension of the hypothesis list of the goal. To highlight the new hypotheses and to save space, we will show only the new hypotheses in the subgoals. Also, we will not explicitly display trivial extraction terms, that is, extraction terms which are just axiom.ATOM
formation
1.![]() »
»  ext atom by intro atom
ext atom by intro atom
2.![]() » atom in
» atom in  by intro
by intro
canonical
3."" by intro ""
4.![]() »
» "![]()
" in atom by intro
5.![]() » atom_eq(
» atom_eq(![]() ;
;![]() ;
;![]() ;
;![]() ) in
) in ![]() by intro
by intro
» ![]() in atom
in atom
» ![]() in atom
in atom
![]() =
=![]() in atom »
in atom » ![]() in
in ![]()
(![]() =
=![]() in atom)->void »
in atom)->void » ![]() in
in ![]()
computation
6a.»
6b.![]() » atom_eq(
» atom_eq(![]() ;
;![]() ;
;![]() ;
;![]() )=
)=![]() in
in ![]() by reduce 1
by reduce 1
» ![]() =
=![]() in
in ![]()
where ![]() and
and ![]() are different canonical token terms.
are different canonical token terms.
VOID
formation
1. ext void by intro void
ext void by intro void
2.![]() » void in
» void in  by intro
by intro
noncanonical
3.
4.![]() » any(
» any(![]() ) in
) in ![]() by intro
by intro
» ![]() in void
in void
INT
formation
1. ext int by intro int
ext int by intro int
2.![]() » int in
» int in  by intro
by intro
canonical
3.
4.![]() »
» ![]() in int by intro
in int by intro
where
noncanonical
5.»
6.![]() » int ext
» int ext ![]() by intro
by intro ![]()
» int ext ![]()
» int ext ![]()
7.![]() »
» ![]() in int by intro
in int by intro
» ![]() in int
in int
» ![]() in int
where
in int
where ![]() must be one of +,-,*,/, or mod.
must be one of +,-,*,/, or mod.
8.![]() ,
,![]() :int,
:int,![]() »
» ![]() ext ind(
ext ind(![]() ;
;![]() .
.![]() ;
;![]() ;
;![]() .
.![]() )
by elim
)
by elim ![]() new
new ![]() [,
[,![]() ]
]
![]() :int,
:int,![]() <0,
<0,![]() :
:![]() [
[![]() +1/
+1/![]() ]
»
]
» ![]() [
[![]() /
/![]() ] ext
] ext ![]()
» ![]() [0/
[0/![]() ] ext
] ext ![]()
![]() :int,0<
:int,0<![]() ,
,![]() :
:![]() [
[![]() -1/
-1/![]() ]
»
]
» ![]() [
[![]() /
/![]() ] ext
] ext ![]()
The optional new name must be given if
9.![]() » ind(
» ind(![]() ;
;![]() ,
,![]() .
.![]() ;
;![]() ;
;![]() ,
,![]() .
.![]() ) in
) in ![]()
by intro [over ![]() .
.![]() ] [new
] [new ![]() ,
,![]() ]
]
» ![]() in int
in int
![]() :int,
:int,![]() <0,
<0,![]() :
:
![]() »
» ![]() in
in ![]()
» ![]() in
in ![]()
![]() :int,0<
:int,0<![]() ,
,![]() :
:
![]() »
» ![]() in
in ![]()
10.![]() » int_eq(
» int_eq(![]() ;
;![]() ;
;![]() ;
;![]() ) in
) in ![]() by intro
by intro
» ![]() in int
in int
» ![]() in int
in int
![]() =
=![]() in int »
in int » ![]() in
in ![]()
(![]() =
=![]() in int)->void »
in int)->void » ![]() in
in ![]()
11.![]() » less(
» less(![]() ;
;![]() ;
;![]() ;
;![]() ) in
) in ![]() by intro
by intro
» ![]() in int
in int
» ![]() in int
in int
![]() <
<![]() »
» ![]() in
in ![]()
(![]() <
<![]() )->void »
)->void » ![]() in
in ![]()
computation
12a.»
»
12b.![]() » ind(
» ind(![]() ;
;![]() ,
,![]() ./
./![]() ;
;![]() ;
;![]() ,
,![]() .
.![]() ) =
) = ![]() in
in ![]() by reduce 1 base
by reduce 1 base
» ![]() =
= ![]() in
in ![]()
» ![]() = 0 in int
= 0 in int
12c.![]() » ind(
» ind(![]() ;
;![]() ,
,![]() .
.![]() ;
;![]() ;
;![]() ,
,![]() .
.![]() ) =
) = ![]() in
in ![]() by reduce 1 up
by reduce 1 up
» ![]() [
[![]() ,(ind(
,(ind(![]() -1;
-1;![]() ,
,![]() .
.![]() ;
;![]() ;
;![]() ,
,![]() .
.![]() ))/
))/![]() ,
,![]() ] =
] = ![]() in
in ![]()
» 0<![]()
13a.![]() » int_eq(
» int_eq(![]() ;
;![]() ;
;![]() ;
;![]() ) =
) = ![]() in
in ![]() by reduce 1
by reduce 1
» ![]() =
=![]() in
in ![]()
13b.![]() » int_eq(
» int_eq(![]() ;
;![]() ;
;![]() ;
;![]() ) =
) = ![]() in
in ![]() by reduce 1
by reduce 1
» ![]() =
= ![]() in
in ![]()
where ![]() and
and ![]() are canonical int terms, and
are canonical int terms, and ![]() .
.
14a.![]() » less(
» less(![]() ;
;![]() ;
;![]() ;
;![]() ) =
) = ![]() in
in ![]() by reduce 1
by reduce 1
» ![]() =
=![]() in
in ![]()
where ![]() and
and ![]() are canonical int terms such that
are canonical int terms such that ![]() .
.
14b.![]() » less(
» less(![]() ;
;![]() ;
;![]() ;
;![]() ) =
) = ![]() in
in ![]() by reduce 1
by reduce 1
» ![]() =
=![]() in
in ![]()
where ![]() and
and ![]() are canonical int terms such that
are canonical int terms such that ![]() .
.
LESS
formation
1. ext
ext
2.![]() »
» ![]() <
<![]() in
in  by intro
by intro
![]() »
» ![]() in int
in int
![]() »
» ![]() in int
in int
equality
3.
LIST
formation
1. ext
ext »
 ext
ext
2.![]() »
» ![]() list in
list in  by intro
by intro
» ![]() in
in 
canonical
3.
»

4.![]() » nil in
» nil in ![]() list by intro at
list by intro at 
» ![]() in
in 
5.![]() »
» ![]() list ext
list ext ![]() .
.![]() by intro .
by intro .
» ![]() ext
ext ![]()
» ![]() list ext
list ext ![]()
6.![]() »
» ![]() in
in ![]() list by intro
list by intro
» ![]() in
in ![]()
» ![]() in
in ![]() list
list
noncanonical
7.by elim
»
8.![]() » list_ind(
» list_ind(![]() ;
;![]() ;
;![]() ) in
) in ![]() [
[![]() /
/![]() ]
]
by intro [over ![]() ] using
] using ![]() list [new u,v,w]
list [new u,v,w]
» ![]() in
in ![]() list
list
» ![]() in
in ![]() [nil/
[nil/![]() ]
]
![]() :
:![]() ,
,![]() :
:![]() list,
list,![]() :
:![]() [
[![]() /
/![]() ]
]
» ![]() [
[![]() /
/![]() ] in
] in
![]() [
[![]() .
.![]() /
/![]() ]
]
computation
9a.»
9b.![]() » list_ind(
» list_ind(![]() ;
;![]() ;
;![]() ) =
) = ![]() in
in ![]() by reduce 1
by reduce 1
» ![]() [
[![]() list_ind(
list_ind(![]() ;
;![]() ;
;![]() )/
)/![]() ]
=
]
= ![]() in
in ![]()
UNION
formation
1. ext
ext »
 ext
ext »
 ext
ext
2.![]() »
» ![]() |
|![]() in
in  by intro
by intro
» ![]() in
in 
» ![]() in
in 
canonical
3. left
left
»
»

4.![]() » inl(
» inl(![]() ) in
) in ![]() |
|![]() by intro at
by intro at 
» ![]() in
in ![]()
» ![]() in
in 
5.![]() »
» ![]() |
|![]() ext inr(
ext inr(![]() ) by intro at
) by intro at  right
right
» ![]() ext
ext ![]()
» ![]() in
in 
6.![]() » inr(
» inr(![]() ) in
) in ![]() |
|![]() by intro at
by intro at 
» ![]() in
in ![]()
» ![]() in
in 
noncanonical
7.
8.![]() » decide(
» decide(![]() ;
;![]() .
.![]() ;
;![]() .
.![]() ) in
) in ![]() [
[![]() /
/![]() ]
]
by intro [over ![]() .
.![]() ] using
] using ![]() |
|![]() [new u,v]
[new u,v]
» ![]() in
in ![]() |
|![]()
![]() :
:![]() ,
, ![]() =inl(
=inl(![]() ) in
) in ![]() |
|![]() »
»
![]() [
[![]() /
/![]() ] in
] in ![]() [inl(
[inl(![]() )/
)/![]() ]
]
![]() :
:![]() ,
, ![]() =inr(
=inr(![]() ) in
) in ![]() |
|![]() »
»
![]() [
[![]() /
/![]() ] in
] in ![]() [inr(
[inr(![]() )/
)/![]() ]
]
computation
9a.»
9b.![]() » decide(inr(
» decide(inr(![]() );
);![]() .
.![]() ;
;![]() .
.![]() ) =
) = ![]() in
in ![]() by reduce 1
by reduce 1
» ![]() [
[![]() /
/![]() ] =
] = ![]() in
in ![]()
FUNCTION
formation
1. ext
ext »

 ext
ext
2.![]() »
» ![]() :
:![]() ->
->![]() in
in  by intro [new
by intro [new ![]() ]
]
» ![]() in
in 
![]() :
:![]() »
» ![]() [
[![]() /
/![]() ] in
] in 
3.![]() »
»  ext
ext ![]() ->
->![]() by intro function
by intro function
»  ext
ext ![]()
»  ext
ext ![]()
4.![]() »
» ![]() ->
->![]() in
in  by intro
by intro
» ![]() in
in 
» ![]() in
in 
canonical
5. [new
[new »

6.![]() »
» ![]()
![]() .
.![]() in
in ![]() :
:![]() ->
->![]() by intro at
by intro at  [new
[new ![]() ]
]
![]() :
:![]() »
» ![]() [
[![]() /
/![]() ] in
] in ![]() [
[![]() /
/![]() ]
]
» ![]() in
in 
noncanonical
7.
8.![]() ,
,![]() :(
:(![]() :
:![]() ->
->![]() ),
),![]() »
» ![]() ext
ext ![]() [
[![]() (
(![]() )/
)/![]() ]
by elim
]
by elim ![]() [new
[new ![]() ]
]
» ![]() ext
ext ![]()
![]() :
:![]() »
» ![]() ext
ext ![]()
The first form is used when ![]() occurs free in
occurs free in ![]() , the second when it
doesn't.
, the second when it
doesn't.
9.![]() »
» ![]() (
(![]() ) in
) in ![]() [
[![]() /
/![]() ] by intro using
] by intro using ![]() :
:![]() ->
->![]()
» ![]() in
in ![]() :
:![]() ->
->![]()
» ![]() in
in ![]()
equality
10.»
»
computation
11.»
PRODUCT
formation
1. ext
ext »

 ext
ext
2.![]() »
» ![]() :
:![]() #
#![]() in
in  by intro [new
by intro [new ![]() ]
]
» ![]() in
in 
![]() :
:![]() »
» ![]() [
[![]() /
/![]() ] in
] in 
3.![]() »
»  ext
ext ![]() #
#![]() by intro product
by intro product
»  ext
ext ![]()
»  ext
ext ![]()
4.![]() »
» ![]() #
#![]() in
in  by intro
by intro
» ![]() in
in 
» ![]() in
in 
canonical
5.
»
»

6.![]() » <
» <![]() ,
,![]() > in
> in ![]() :
:![]() #
#![]() by intro at
by intro at  [new
[new ![]() ]
]
» ![]() in
in ![]()
» ![]() in
in ![]() [
[![]() /
/![]() ]
]
![]() :
:![]() »
» ![]() [
[![]() /
/![]() ] in
] in 
7.![]() »
» ![]() #
#![]() ext <
ext <![]() ,
,![]() > by intro
> by intro
» ![]() ext
ext ![]()
» ![]() ext
ext ![]()
8.![]() » <
» <![]() ,
,![]() > in
> in ![]() #
#![]() by intro
by intro
» ![]() in
in ![]()
» ![]() in
in ![]()
noncanonical
9.
10.![]() » spread(
» spread(![]() ;
;![]() ) in
) in ![]() [
[![]() /
/![]() ]
]
by intro [over ![]() ] using
] using ![]() :
:![]() #
#![]() [new
[new ![]() ]
]
» ![]() in
in ![]() :
:![]() #
#![]()
![]() :
:![]() ,
,![]() :
:![]() [
[![]() /
/![]() ],
],![]() =<
=<![]() ,
,![]() > in
> in ![]() :
:![]() #
#![]() »
»
![]() [
[![]() /
/![]() ] in
] in ![]() [<
[<![]() ,
,![]() >/
>/![]() ]
]
computation
11.»
QUOTIENT
formation
1. ext (
ext (»


2.![]() » (
» (![]() ):
):![]() //
//![]() in
in  by intro new
by intro new ![]() ,
,![]() ,
,![]()
» ![]() in
in 
![]() :
:![]() ,
,![]() :
:![]() »
» ![]() [
[![]() /
/![]() ] in
] in 
![]() :
:![]() »
» ![]() [
[![]() /
/![]() ]
]
![]() :
:![]() ,
,![]() :
:![]() ,
,![]() [
[![]() /
/![]() ]
»
]
» ![]() [
[![]() /
/![]() ]
]
![]() :
:![]() ,
,![]() :
:![]() ,
,![]() :
:![]() ,
,![]() [
[![]() /
/![]() ],
], ![]() [
[![]() /
/![]() ] »
] » ![]() [
[![]() /
/![]() ]
]
canonical
3.
» (

»
4.![]() »
» ![]() in (
in (![]() ):
):![]() //
//![]() by intro at
by intro at 
» (![]() ):
):![]() //
//![]() in
in 
» ![]() in
in ![]()
noncanonical
5. [new
[new 
»

equality
6. by intro [new
by intro [new » (

» (

»

 ,
, ,
,
7.![]() »
» ![]() =
= ![]() in (
in (![]() ):
):![]() //
//![]() by intro at
by intro at 
» (![]() ):
):![]() //
//![]() in
in 
» ![]() in
in ![]()
» ![]() in
in ![]()
» ![]() [
[![]() /
/![]() ]
]
SET
formation
< 1. ext
ext 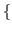
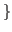 by intro set
by intro set »

 ext
ext
2.![]() »
» 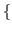
![]() :
:![]() |
|![]()
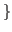 in
in  by intro [new y]
by intro [new y]
» ![]() in
in 
![]() :
:![]() »
» ![]() [
[![]() /
/![]() ] in
] in 
3.![]() »
»  ext
ext 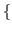
![]() |
|![]()
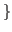 by intro set
by intro set
»  ext
ext ![]()
»  ext
ext ![]()
4.![]() »
» 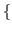
![]() |
|![]()
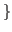 in
in  by intro
by intro
» ![]() in
in 
» ![]() in
in 
canonical
5.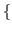
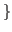 ext
ext 
»
»

All hidden hypothesis in ![]() become unhidden in the second
subgoal.
become unhidden in the second
subgoal.
6.![]() »
» ![]() in
in 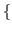
![]() :
:![]() |
|![]()
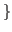 by intro at
by intro at  [new
[new ![]() ]
]
» ![]() in
in ![]()
» ![]() [
[![]() /
/![]() ]
]
![]() :
:![]() »
» ![]() [
[![]() /
/![]() ] in
] in 
7.![]() »
» 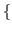
![]() |
|![]()
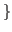 ext
ext ![]() by intro
by intro
» ![]() ext
ext ![]()
» ![]() ext
ext ![]()
8.![]() »
» ![]() in
in 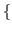
![]() |
|![]()
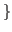 by intro
by intro
» ![]() in
in ![]()
» ![]() ext
ext ![]()
noncanonical
9.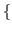
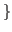 ,
, [new
[new 
Note that the second new hypotheses of the second subgoal is hidden.
equality
10.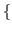
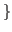 =
= 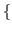
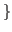 in
in  by intro [new
by intro [new »

EQUALITY
formation
1. ext
ext »

»
»
The default for ![]() is 1.
is 1.
2.![]() » (
» (![]() =
=![]() =
=![]() in
in ![]() ) in
) in  by intro
by intro
» ![]() in
in 
» ![]() in
in ![]()
![]()
» ![]() in
in ![]()
canonical
3.»
4.![]() ,
,![]() :
:![]() ,
,![]() »
» ![]() in
in ![]() by intro
by intro
This rule doesn't work when T is a set or quotient term, since intro will invoke the equality rule for the set or quotient type, respectively. In any case, the equality rule can be used.
UNIVERSE
canonical
1. ext
ext 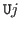 by intro universe
by intro universe 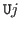
2.![]() »
» 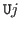 in
in  by intro
by intro
where
noncanonical
Currently there are no rules in the system for analyzing universes. At some later date such rules may be added.
MISCELLANEOUS
hypothesis
1.where ![]() is
is ![]() -convertible to
-convertible to ![]()
sequence
2.by seq
»
lemma
3.where ![]() is the conclusion of the complete theorem
is the conclusion of the complete theorem ![]() .
.
def
4.where ![]() is the conclusion of the complete theorem,
is the conclusion of the complete theorem, ![]() ,
and
,
and ![]() -
-![]() is the term extracted from that theorem.
8.10
is the term extracted from that theorem.
8.10
explicit intro
5.»
cumulativity
6. by cumulativity at
by cumulativity at 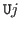
»
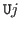
where ![]()
substitution
7.
»
»

direct computation
8.»
9.![]() ,
, ![]() :
:![]() ,
, ![]() »
» ![]() ext
ext ![]() by compute hyp i using
by compute hyp i using ![]()
![]() ,
, ![]() :
:![]() ,
, ![]() »
» ![]() ext
ext ![]()
where ![]() :
:![]() is the
is the ![]() hypothesis, where
hypothesis, where ![]() is
obtained from
is
obtained from ![]() by ``tagging'' some of its subterms, and
where
by ``tagging'' some of its subterms, and
where ![]() is generated by the system by performing some
computation steps on subterms of
is generated by the system by performing some
computation steps on subterms of ![]() , as indicated by the
tags. A subterm
, as indicated by the
tags. A subterm ![]() is tagged by replacing it by
[[*;
is tagged by replacing it by
[[*;![]() ]] or [[
]] or [[![]() ;
;![]() ]], where
]], where ![]() is a positive
integer constant. The latter tag causes
is a positive
integer constant. The latter tag causes ![]() to be computed
for
to be computed
for ![]() steps, and the former causes computation to proceed
as far as possible. There are some somewhat complicated
restrictions on what subterms of
steps, and the former causes computation to proceed
as far as possible. There are some somewhat complicated
restrictions on what subterms of ![]() may be tagged, but most
users will likely find it sufficient to know that any subterm
of
may be tagged, but most
users will likely find it sufficient to know that any subterm
of ![]() may be tagged that does not occur within the scope of
a binding variable occurrence in
may be tagged that does not occur within the scope of
a binding variable occurrence in ![]() . An application of
one of these
rules will fail if the tagging is illegal, or if removing the
tags from
. An application of
one of these
rules will fail if the tagging is illegal, or if removing the
tags from ![]() does not yield a term equal to
does not yield a term equal to ![]() . For a more
complete description of this rule, see appendix C.
Note that many of the computation rules, such as the one for product,
are instances of direct computation.
. For a more
complete description of this rule, see appendix C.
Note that many of the computation rules, such as the one for product,
are instances of direct computation.
equality
10.where the equality of ![]() and
and ![]() can be deduced from assumptions that are
equalities over
can be deduced from assumptions that are
equalities over ![]() (or equalities over
(or equalities over ![]() where
where ![]() is deducible
using only reflexivity, commutativity and transitivity)
.
is deducible
using only reflexivity, commutativity and transitivity)
.
arith
11.
The arith rule is used to justify conclusions which follow from
hypotheses by
a restricted form of arithmetic reasoning. Roughly speaking, arith knows
about the ring axioms for integer multiplication and addition, the total
order axioms of ![]() , the reflexivity, symmetry and transitivity of equality, and
a limited form of substitutivity of equality. We will describe the class
of problems decidable by arith by giving an informal account of the
procedure which arith uses to decide whether or not
, the reflexivity, symmetry and transitivity of equality, and
a limited form of substitutivity of equality. We will describe the class
of problems decidable by arith by giving an informal account of the
procedure which arith uses to decide whether or not ![]() follows from
follows from ![]() .
.
The terms that arith understands are those denoting arithmetic relations,
namely terms of the form ![]() <
<![]() ,
, ![]() =
=![]() in int
or the negation of a term of this form.
As the only equalities arith concerns itself with are those of the form
in int
or the negation of a term of this form.
As the only equalities arith concerns itself with are those of the form
![]() =
=![]() in int, we will drop the in int and write only
in int, we will drop the in int and write only
![]() =
=![]() in the rest of this description.
For arith the negation of an arithmetic relation
in the rest of this description.
For arith the negation of an arithmetic relation ![]() where
where
![]() is one of
is one of ![]() or
or ![]() is of the form
(
is of the form
(![]() )->void, which we will write as
)->void, which we will write as
![]() .
As integer equality and less-than are decidable relations,
.
As integer equality and less-than are decidable relations,
![]() and
and
![]() denote the same relation and will be treated identically by arith.
denote the same relation and will be treated identically by arith.
The arith rule may be used to justify goals of the form
![]() ,
, ![]() ,
, ![]() »
» ![]() |
| ![]() |
| ![]() ,
,
where each ![]() and
and ![]() is a term denoting an arithmetic relation.
If arith can justify the goal it will produce subgoals requiring the user
to show that the left- and right-hand sides of each
is a term denoting an arithmetic relation.
If arith can justify the goal it will produce subgoals requiring the user
to show that the left- and right-hand sides of each ![]() denote integer
terms.
As a convenience arith will attempt to prove goals in which not all of the
denote integer
terms.
As a convenience arith will attempt to prove goals in which not all of the
![]() are arithmetic relations; it simply ignores such disjuncts. If it is
successful on such a goal, it will produce subgoals
requiring the user to prove that each such disjunct is a type
at the level given in the invocation of the rule.
are arithmetic relations; it simply ignores such disjuncts. If it is
successful on such a goal, it will produce subgoals
requiring the user to prove that each such disjunct is a type
at the level given in the invocation of the rule.
Arith begins by normalizing the relevant formulas of the goal according to the following conventions:
- Rewrite each relation of the form
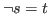 as the
equivalent
as the
equivalent 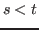 |
|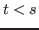 .
A conclusion
.
A conclusion 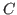 follows from such an
assumption if it follows from either
follows from such an
assumption if it follows from either 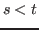 or
or 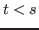 ; hence arith
tries both cases.
Henceforth, we assume that all negations of equalities have been
eliminated from consideration.
; hence arith
tries both cases.
Henceforth, we assume that all negations of equalities have been
eliminated from consideration.
- Replace all occurrences of terms which are not addition, subtraction
or multiplication by a new variable.
Multiple occurrences of the same term are replaced by the same variable.
Arith uses only facts about addition, subtraction and multiplication,
so it
treats all other terms as atomic.
At this point all terms are built from integer constants and integer
variables using
 ,
,  and
and 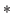 .
.
- Rewrite all terms as polynomials
in canonical form. The exact
nature of the canonical form is irrelevant (the reader may think
of it as the form used in high school algebra texts) but has the
important property that any two equal terms are identical.
Each term now has the form
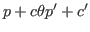 , where
, where  and
and  are nonconstant polynomials in
canonical form,
are nonconstant polynomials in
canonical form, 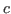 and
and 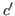 are
constants, and
are
constants, and 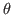 is one of
is one of  ,
, 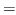 or
or 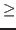 (
(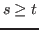 is
equivalent to
is
equivalent to 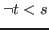 ).
).
- Replace each nonconstant polynomial
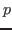 by a new variable,
with each occurrence of
by a new variable,
with each occurrence of 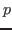 being replaced by the same variable.
This amounts to treating each nonconstant polynomial as an atom.
Now each formula is of the form
being replaced by the same variable.
This amounts to treating each nonconstant polynomial as an atom.
Now each formula is of the form
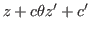 .
Arith now decides whether or not the conclusion follows from the hypotheses
by using the total order axioms of
.
Arith now decides whether or not the conclusion follows from the hypotheses
by using the total order axioms of 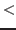 , the reflexivity, symmetry,
transitivity and substitutivity of
, the reflexivity, symmetry,
transitivity and substitutivity of 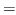 , and the following so-called
trivial monotonicity axioms (
, and the following so-called
trivial monotonicity axioms (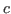 and
and 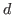 are constants).
are constants).
-
For a detailed account of the arith rule and a proof of its correctness, see the article by Tat-hung Chan in [Constable, Johnson, & Eichenlaub 82].
ML Constructors
One of the features of the Nuprl system is that it comes with its own formal metalanguage, implemented in ML. Accordingly, ML needs access to the rules of the system. Following is a list of the ML rule constructors. The constructors are categorized and numbered in the same manner as the rules. For example, the constructor numbered 4 in the atom section corresponds to the rule numbered 4 in the atom section. Each constructor is presented in the form constructor_name(parameter names): type. The parameter names are never actually used but appear here solely for documentation purposes. Following are some conventions regarding the parameter names which we give with their types:
- hyp:int is used to indicate a hypothesis.
- where:int is used to indicate which equand of an equality should be reduced in a computation rule.
- level:int is used to give a universe level.
- using:term is used to indicate a using term.
- over_id:tok, over:term are used to indicate an over term. If the over_id is the token `nil`, the over term is ignored.
Unlike the rules, each constructor needs a unique name. The general form of the names is base-type_kind_qualifier, where base-type is a prl type and kind is one of intro, elim, equality, formation or computation. So, for example, list_equality_nil is the name of the constructor for the rule which specifies how to show two nil terms are the same in a list type, and int_elim is the name of the constructor for the elim rule for integers. There are some exceptions to this general pattern, the main one being that the name of the constructor for the rule for showing two canonical type terms to be equal in some universe is type_equality rather than universe_equality_type.
ATOM
formation universe_intro_atom: rule.
atom_equality: rule.
canonical
atom_intro(token): term ![]() rule.
rule.
atom_equality_token: rule.
quality
atom_eq_equality: rule.
computation
atom_eq_computation(where): intVOID
formation
universe_intro_void: rule.void_equality: rule.
noncanonical
void_elim(hyp): intvoid_equality_any: rule.
INT
formation
universe_intro_integer: rule.int_equality: rule.
canonical
integer_intro_integer(c): intinteger_equality_natural_number: rule.
noncanonical
integer_equality_minus: rule.
integer_intro_addition: rule.
integer_intro_subtraction: rule.
integer_intro_multiplication: rule.
integer_intro_division: rule.
integer_intro_modulo: rule.
integer_equality_addition: rule.
integer_equality_subtraction: rule.
integer_equality_multiplication: rule.
integer_equality_division: rule.
integer_equality_modulo: rule.
integer_elim(hyp y z): int ![]() tok
tok ![]() tok
tok ![]() rule.
rule.
integer_equality_induction(over_id over u v):
tok ![]() term
term ![]() tok
tok ![]() tok
tok ![]() rule.
rule.
equality
int_eq_equality: rule.int_less_equality: rule.
computation
integer_computation(kind where): tok
int_eq_computation(where): int ![]() rule.
rule.
int_less_computation(where): int ![]() rule.
rule.
LESS
formation
universe_intro_less: rule.less_equality: rule.
equality
axiom_equality_less: rule.LIST
formation
universe_intro_list: rule.
list_equality(level): int ![]() rule.
rule.
canonical
list_intro_nil(level): int
list_equality_nil(level): int ![]() rule.
rule.
list_intro_cons: rule.
list_equality_cons: rule.
noncanonical
list_elim (hyp u v w): int
list_equality_induction (over_id over using u v w):
tok ![]() term
term ![]() term
term ![]() tok
tok ![]() tok
tok ![]() tok
tok ![]() rule.
rule.
computation
list_computation(where): intUNION
formation
universe_intro_union: rule.union_equality: rule.
canonical
union_intro_left(level): int
union_equality_inl(level): int ![]() rule.
rule.
union_intro_right(level): int ![]() rule.
rule.
union_equality_inr(level): int ![]() rule.
rule.
noncanonical
union_elim(hyp x y): int
union_equality_decide(over_id over using u v):
tok ![]() term
term ![]() term
term ![]() tok
tok ![]() tok
tok ![]() rule.
rule.
computation
union_computation(where): intFUNCTION
formation
universe_intro_function(x term): tok
function_equality(y): tok ![]() rule.
rule.
universe_intro_function_independent: rule.
function_equality_independent: rule.
canonical
function_intro(level y): int
function_equality_lambda(level z): int ![]() tok
tok ![]() rule.
rule.
noncanonical
function_elim(hyp on y): int
function_elim_independent(hyp y): int ![]() tok
tok ![]() rule.
rule.
function_equality_apply(using): term ![]() rule.
rule.
equality
extensionality(y): tok
computation
function_computation(where): intPRODUCT
formation
universe_intro_product(x left_term): tok
product_equality(y): tok ![]() rule.
rule.
universe_intro_product_independent: rule.
product_equality_independent: rule.
canonical
product_intro_dependent(left_term level y): term
product_equality_pair(level y): int ![]() tok
tok ![]() rule.
rule.
product_intro: rule.
product_equality_pair_independent: rule.
noncanonical
product_elim(hyp u v): int
product_equality_spread(over_id over using u v):
tok ![]() term
term ![]() term
term ![]() tok
tok ![]() tok
tok ![]() rule.
rule.
computation
product_computation(where): intQUOTIENT
formation
universe_intro_quotient(A E x y z): term
quotient_formation(x y z): tok ![]() tok
tok ![]() tok
tok ![]() rule.
rule.
canonical
quotient_intro(level): int
quotient_equality_element(level): int ![]() rule.
rule.
noncanonical
quotient_elim (hyp level v w): int
equality
quotient_equality(r s): tok
quotient_equality_element(level): int ![]() rule.
rule.
SET
formation
universe_intro_set(x type): tok
set_formation(y): tok ![]() rule.
rule.
universe_intro_set_independent: rule.
set_formation_independent: rule.
canonical
set_intro(level left_term y): int
set_equality_element(level y): int ![]() tok
tok ![]() rule.
rule.
set_intro_independent: rule.
set_equality_element: rule.
noncanonical
set_elim(hyp level y): int
equality
set_equality(z): tokEQUALITY
formation
universe_intro_equality(type number_terms): termequal_equality: rule.
canonical
axiom_equality_equal: rule.equal_equality_variable: rule.
UNIVERSE
canonical
universe_intro_universe (level): intuniverse_equality: rule.
MISCELLANEOUS
hypothesis
hyp(hyp): int
sequence
seq(term_list id_list): (term list)
lemma
lemma(lemma_name x): tok
def
def(theorem x): tok
explicit intro
explicit_intro(term): term
cumulativity
cumulativity(level): int
substitution
substitution(level equality_term over_id over): int
direct computation
direct_computation(tagged_term): term
direct_computation_hyp(hyp tagged_term):
int ![]() term
term ![]() rule.
rule.
equality
equality: rule.
arith
arith(level): intFootnotes
- ....8.1
- There is a similarity between a type and Bishop's notion of set. Bishop [Bishop 67] says that to give a set, one gives a way to construct its members and gives an equivalence relation, called the equality on that set, on the members.
- ... variables.8.2
- An identifier is any string of letters, digits, underscores or at-signs that starts with a letter. The only identifiers which cannot be used for variables are term_of and those which serve as operator names, such as int or spread.
- ....8.3
- In the
formation of these as members of
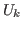 ,
, 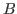 must be
must be
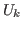 -functional in
-functional in 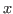 :
: .
.
- ... constructor.8.4
- modulo the difference between
 #
#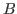 and
and 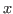 :
: #
#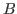 , etc.
, etc.
- ... CLASS="MATH">
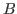 ).8.5
).8.5 -
If the reader finds this a bit difficult to follow, perhaps it would help
to consider first the case in which
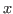 is not free in
is not free in 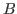 and
and 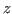 is not free in
is not free in 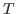 and then the more general cases afterward.
and then the more general cases afterward.
- ... integers.8.6
- This is defined by primitive recursion with 0 as the base case and an induction step for each direction out (positive and negative). Of course, in a higher-order system such as Nuprl, where functions can take functions as arguments and have functions as values, one can define by primitive recursion functions in int->int which are not primitive recursive.
- ... true.8.7
- If we were to give a similar semantic account of the judgements of [Martin-Löf 82], the plainest difference between the truth conditions for those judgements and Nuprl judgements would be that the truth of the former requires type-functionality of each assumption in all its variables.
- ... inhabited.8.8
-
Recall that the term (
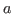 =
= 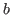 in
in  )
is a type whenever
)
is a type whenever 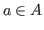 and
and 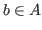 and is inhabited just when
and is inhabited just when
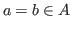 .
As a special case, the term (
.
As a special case, the term (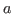 in
in  ) is a type and is inhabited
just when
) is a type and is inhabited
just when 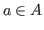 .
.
- ... system.8.9
- It turns out that these predicates will hold only for closed terms.
- ... theorem.8.10
- This rule introduces very strong interproof dependencies.
A proof using this rule depends not only on
 but also on the way
but also on the way
 is proved.
is proved.