| | Some definitions of interest. |
|
| assert | Def 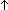 b == if b b == if b True else False fi True else False fi |
| | | Thm*  b: b: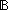 . b . b  Prop Prop |
|
| band | Def p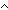 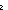 q == if p q == if p q else false q else false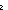 fi fi |
| | | Thm*  p,q: p,q: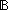 . (p . (p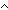 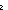 q) q)  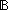 |
|
| decidable | Def Dec(P) == P 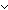 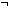 P P |
| | | Thm*  A:Prop. Dec(A) A:Prop. Dec(A)  Prop Prop |
|
| iff | Def P 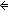  Q == (P Q == (P   Q) & (P Q) & (P 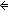  Q) Q) |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A 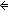  B) B)  Prop Prop |
|
| sfa_doc_greater_list_bound | Def y greater-bounds x ==  i: i: ||x||. x[i]<y ||x||. x[i]<y |
| | | Thm*  x: x: List, y: List, y: . y greater-bounds x . y greater-bounds x  Prop Prop |
|
| int_seg | Def {i..j } == {k: } == {k: | i | i 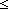 k < j } k < j } |
| | | Thm*  m,n: m,n: . {m..n . {m..n } }  Type Type |
|
| kleene_minimize | Def mu(f) == if f(0) 0 else 1+mu( 0 else 1+mu(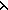 x.f(1+x)) fi (recursive) x.f(1+x)) fi (recursive) |
| | | Thm* mu  {f:( {f:(   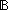 )| )| 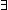 x: x: . f(x) } . f(x) }   |
|
| nat | Def  == {i: == {i: | 0 | 0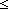 i } i } |
| | | Thm*   Type Type |
|
| le | Def A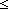 B == B == 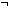 B<A B<A |
| | | Thm*  i,j: i,j: . (i . (i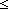 j) j)  Prop Prop |
|
| nequal | Def a 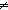 b b  T == T == 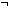 a = b a = b  T T |
| | | Thm*  A:Type, x,y:A. (x A:Type, x,y:A. (x 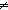 y) y)  Prop Prop |
|
| sfa_doc_factorial | Def x! == if x=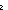 0 0 1 else x 1 else x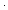 (x-1)! fi (recursive) (x-1)! fi (recursive) |
| | | Thm*  x: x: . x! . x!   |
|
| sfa_doc_ntuple | Def A^n == if n=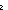 0 0 Unit ; n= Unit ; n=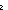 1 1 A else A A else A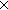 (A^(n-1)) fi (recursive) (A^(n-1)) fi (recursive) |
| | | Thm*  A:Type, n: A:Type, n: . (A^n) . (A^n)  Type Type |
|
| sfa_doc_sample_intmod | Def  mod k == x,y: mod k == x,y: //( //(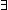 m: m: . x-y = m . x-y = m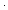 k) k) |
| | | Thm*  k: k: . .  mod k mod k  Type Type |
|
| sfa_doc_sexpr | Def Sexpr(A) == rec(T.(T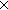 T)+A) T)+A) |
| | | Thm*  A:Type. Sexpr(A) A:Type. Sexpr(A)  Type Type |
|
| sfa_doc_sexpr_reverse | Def Reverse(e)
Def == Case of e
Def == CaInj(x)  Inj(x) Inj(x)
Def == CaCons(s1;s2)  Cons(Reverse(s2);Reverse(s1)) Cons(Reverse(s2);Reverse(s1))
Def (recursive) |
| | | Thm*  A:Type, e:Sexpr(A). Reverse(e) A:Type, e:Sexpr(A). Reverse(e)  Sexpr(A) Sexpr(A) |
|
| sfa_doc_sexpr_cons | Def Cons(s1;s2) == inl(<s1,s2>) |
| | | Thm*  A:Type, s1,s2:Sexpr(A). Cons(s1;s2) A:Type, s1,s2:Sexpr(A). Cons(s1;s2)  Sexpr(A) Sexpr(A) |
|
| sfa_doc_sexpr_inj | Def Inj(a) == inr(a) |
| | | Thm*  A:Type, a:A. Inj(a) A:Type, a:A. Inj(a)  Sexpr(A) Sexpr(A) |
|
| subtype | Def S 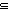 T == T ==  x:S. x x:S. x  T T |
|
| top | Def Top == Void(given Void) |
| | | Thm* Top  Type Type |