| 1 | 16.  x,y:Alph*.
(Result(Auto)x) = (Result(Auto)y) x,y:Alph*.
(Result(Auto)x) = (Result(Auto)y) 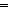  (Result(A(
(Result(A( l:x,y:Alph*//(x LangOf(Auto)-induced Equiv y). true l:x,y:Alph*//(x LangOf(Auto)-induced Equiv y). true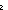 ))x)
=
(Result(A( ))x)
=
(Result(A( l:x,y:Alph*//(x LangOf(Auto)-induced Equiv y). true l:x,y:Alph*//(x LangOf(Auto)-induced Equiv y). true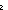 ))y) ))y)
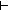 c(Result(Auto)h(b1)) = b2 c(Result(Auto)h(b1)) = b2 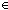 x,y:Alph*//(x LangOf(Auto)-induced Equiv y) x,y:Alph*//(x LangOf(Auto)-induced Equiv y) |