| 1 | 8. ( n@0: n@0: .
( .
( l:Alph*. ||l|| < n@0 l:Alph*. ||l|| < n@0   ( (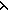 a. a. a':Alph*. ||a'|| < n a':Alph*. ||a'|| < n n & R((a @ b),a' @ b) & R((a @ c),a' @ c))(l)) n & R((a @ b),a' @ b) & R((a @ c),a' @ c))(l))   (
( l:Alph*. ||l|| = n@0 l:Alph*. ||l|| = n@0   ( (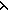 a. a. a':Alph*. ||a'|| < n a':Alph*. ||a'|| < n n & R((a @ b),a' @ b) & R((a @ c),a' @ c))(l))) n & R((a @ b),a' @ b) & R((a @ c),a' @ c))(l)))
  (
( l:Alph*. ( l:Alph*. (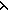 a. a. a':Alph*. ||a'|| < n a':Alph*. ||a'|| < n n & R((a @ b),a' @ b) & R((a @ c),a' @ c))(l)) n & R((a @ b),a' @ b) & R((a @ c),a' @ c))(l))
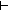  a':Alph*. ||a'|| < n a':Alph*. ||a'|| < n n & R((a @ b),a' @ b) & R((a @ c),a' @ c) n & R((a @ b),a' @ b) & R((a @ c),a' @ c) |