At: fin dec fin 2 1 2 2 4 1 2 2 1 1 2 1 1 1 1
1. n: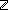 
2. 0 < n
3. 
T:Type, B:(T
Prop).
(
f:(
(n-1)T), g:(T(n-1)). InvFuns((n-1); T; f; g)) & (t:T. Dec(B(t))) 
(m:, f:(m{t:T| B(t) }), g:({t:T| B(t) }m). InvFuns(m; {t:T| B(t) }; f; g))
4. T: Type
5. B: TProp
6. f: nT
7. g: Tn
8. g o f = Id
9. f o g = Id
10. t:T. Dec(B(t))
11. f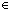 
(n-1){t:T| g(t) < n-1 }
12. g 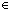{t:T| g(t) < n-1 }(n-1)
13. m:
14. f1: m{t:{t:T| g(t) < n-1 }| B(t) }
15. g@0: {t:{t:T| g(t) < n-1 }| B(t) }m
16. g@0 o f1 = Id
17. f1 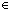m{t:T| B(t) }
18. g@0 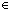{t:T| B(t) }m
19. x: T
20. B(x)
21. z: {t:{t:T| g(t) < n-1 }| B(t) }{t:{t:T| g(t) < n-1 }| B(t) }
22. g(x) = n-1 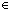n
23. f1 o g@0 = Id 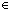{t:{t:T| g(t) < g(x) }| B(t) }{t:{t:T| g(t) < g(x) }| B(t) }
24. 
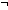B(f(g(x)))
False
By:
RWH (AddrC [1;2] add_composeC) -1
THEN
RWH (HypC 9) -1
THEN
Reduce -1
Generated subgoals:None
About:
