Thm*  R1,R2:(T R1,R2:(T  T T  Prop). ( Prop). ( x,y:T. R1(x,y) x,y:T. R1(x,y)   R2(x,y)) R2(x,y))   Graph(x,y:T. R1(x,y)) Graph(x,y:T. R1(x,y))  Graph(x,y:T. R2(x,y)) Graph(x,y:T. R2(x,y)) | [rel-graph_functionality] |
Thm* For any graph
 A,B,C:V List. A-- > *B @ C A,B,C:V List. A-- > *B @ C   A-- > *B & A-- > *C A-- > *B & A-- > *C | [list-list-connect-append] |
Thm* For any graph
 A:V List, x:V. A-- > *[x] A:V List, x:V. A-- > *[x]   A-- > *x A-- > *x | [list-list-connect-singleton] |
Thm* For any graph
 A,B:V List, i:V. A @ B-- > *i A,B:V List, i:V. A @ B-- > *i   A-- > *i A-- > *i 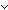 B-- > *i B-- > *i | [list-connect-append] |
Thm* For any graph
 i,j:V. [i]-- > *j i,j:V. [i]-- > *j   i-the_graph- > *j i-the_graph- > *j | [list-connect-singleton] |
Thm* For any graph
( x,y:V. Dec(x = y)) x,y:V. Dec(x = y))   ( ( x,y:V. x-the_graph- > *y x,y:V. x-the_graph- > *y   x = y x = y 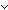 ( ( z:V. z:V.  z = x & x-the_graph- > z & z-the_graph- > *y)) z = x & x-the_graph- > z & z-the_graph- > *y)) | [connect-iff] |
Thm*  E:(T E:(T  T T  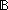 ). ( ). ( x,y:T. E(x,y) x,y:T. E(x,y)   x = y) x = y)   ( ( i:T, s:(T+T) List. member-left-paren(x,y.E(x,y);i;s) i:T, s:(T+T) List. member-left-paren(x,y.E(x,y);i;s)   (inl(i) (inl(i)  s)) s)) | [assert-member-left-paren] |
Thm*  E:(T E:(T  T T  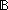 ). ( ). ( x,y:T. E(x,y) x,y:T. E(x,y)   x = y) x = y)   ( ( i:T, s:(T+T) List. member-right-paren(x,y.E(x,y);i;s) i:T, s:(T+T) List. member-right-paren(x,y.E(x,y);i;s)   (inr(i) (inr(i)  s)) s)) | [assert-member-right-paren] |
Thm*  E:(T E:(T  T T  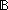 ). ( ). ( x,y:T. E(x,y) x,y:T. E(x,y)   x = y) x = y)   ( ( i:T, s:(T+T) List. member-paren(x,y.E(x,y);i;s) i:T, s:(T+T) List. member-paren(x,y.E(x,y);i;s)   (inl(i) (inl(i)  s) s) 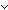 (inr(i) (inr(i)  s)) s)) | [assert-member-paren] |
Thm*  k: k:  , L: , L: List. k-1- > L^k List. k-1- > L^k   ( ( i: i: ||L||. L[i] < k) ||L||. L[i] < k) | [trivial-arrows] |
Thm*  x: x: , n: , n:  . (n | x) . (n | x)   (x mod n) = 0 (x mod n) = 0 | [elim_divides] |
Def dfsl-traversal(the_graph;L;s) == df-traversal(the_graph;s) & ( i:Vertices(the_graph). (inl(i) i:Vertices(the_graph). (inl(i)  s) s)   L-the_graph- > *i) & (( L-the_graph- > *i) & (( i:Vertices(the_graph). L-the_graph- > *i i:Vertices(the_graph). L-the_graph- > *i    non-trivial-loop(the_graph;i)) non-trivial-loop(the_graph;i))   ( ( L1,L2:Vertices(the_graph) List. L = (L1 @ L2) L1,L2:Vertices(the_graph) List. L = (L1 @ L2)   ( ( s1,s2:traversal(the_graph). s = (s2 @ s1) s1,s2:traversal(the_graph). s = (s2 @ s1)  traversal(the_graph) & paren(Vertices(the_graph);s1) & paren(Vertices(the_graph);s2) & ( traversal(the_graph) & paren(Vertices(the_graph);s1) & paren(Vertices(the_graph);s2) & ( j:Vertices(the_graph). ((inl(j) j:Vertices(the_graph). ((inl(j)  s1) s1)   L1-the_graph- > *j) & ((inl(j) L1-the_graph- > *j) & ((inl(j)  s2) s2)   L2-the_graph- > *j & L2-the_graph- > *j &  L1-the_graph- > *j))))) L1-the_graph- > *j))))) | [dfsl-traversal] |