Thm*  n: n: , R:( , R:( n n   n n  Prop), x,y: Prop), x,y: n. (x (R^*) y) n. (x (R^*) y) 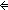  ( ( k: k: (n+1). x R^k y) (n+1). x R^k y) | [rel_star_finite] |
Thm*  R:(T R:(T  T T  Prop), k: Prop), k: , x,y:T. , x,y:T.
Thm* (x R^k y)
Thm* 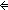 
Thm* ( L:T List. L:T List.
Thm* (||L|| = k+1   & L[0] = x & last(L) = y & ( & L[0] = x & last(L) = y & ( i: i: k. L[i] R L[(i+1)])) k. L[i] R L[(i+1)])) | [rel_exp_list] |
Thm*  L1,L:T List. interleaving(T;L1;nil;L) L1,L:T List. interleaving(T;L1;nil;L) 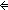  L = L1 L = L1 | [nil_interleaving2] |
Thm*  L1,L:T List. interleaving(T;nil;L1;L) L1,L:T List. interleaving(T;nil;L1;L) 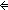  L = L1 L = L1 | [nil_interleaving] |
Thm*  P:(T P:(T  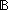 ), T':Type, f:({x:T| P(x) } ), T':Type, f:({x:T| P(x) }  T'), L:T List, x:T'. T'), L:T List, x:T'.
Thm* (x  mapfilter(f;P;L)) mapfilter(f;P;L)) 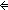  ( ( y:T. (y y:T. (y  L) & P(y) & x = f(y)) L) & P(y) & x = f(y)) | [member_map_filter] |
Thm*  P:(T P:(T  Prop), x:T, L:T List. ( Prop), x:T, L:T List. ( y y [x / L].P(y)) [x / L].P(y)) 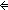  P(x) P(x) 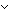 ( ( y y L.P(y)) L.P(y)) | [l_exists_cons] |
Thm*  P:(T P:(T  Prop). ( Prop). ( x x nil.P(x)) nil.P(x)) 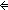  False False | [l_exists_nil] |
Thm*  l:T List, P:(T l:T List, P:(T  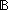 ), x,y:T. ), x,y:T.
Thm* x before y  filter(P;l) filter(P;l) 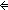  P(x) & P(y) & x before y P(x) & P(y) & x before y  l l | [l_before_filter] |
Thm*  L1,L2:T List, P:(T L1,L2:T List, P:(T  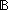 ). L2 ). L2 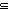 filter(P;L1) filter(P;L1) 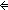  L2 L2 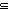 L1 & ( L1 & ( x x L2.P(x)) L2.P(x)) | [sublist_filter] |
Thm*  L:T List, P:(T L:T List, P:(T  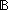 ). ( ). ( x x L.P(x)) L.P(x))   reduce( reduce(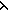 x,y. P(x) x,y. P(x)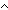 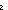 y;true y;true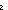 ;L) ;L) | [l_all_reduce] |
Thm*  f:(A f:(A  B), L:A List, P:(B B), L:A List, P:(B  Prop). ( Prop). ( x x map(f;L).P(x)) map(f;L).P(x)) 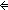  ( ( x x L.P(f(x))) L.P(f(x))) | [l_all_map] |
Thm*  P:(T P:(T  Prop), x:T, L:T List. ( Prop), x:T, L:T List. ( y y [x / L].P(y)) [x / L].P(y)) 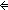  P(x) & ( P(x) & ( y y L.P(y)) L.P(y)) | [l_all_cons] |