| | Some definitions of interest. |
|
| topsort | Def topsort(G) == mapoutl(depthfirst(G)) |
| | | Thm* For any graph
 the_obj:GraphObject(the_graph). topsort(the_obj) the_obj:GraphObject(the_graph). topsort(the_obj)  V List V List |
|
| depthfirst | Def depthfirst(the_obj) == the_obj.vacc(( s,i. dfs(the_obj;s;i)),nil) s,i. dfs(the_obj;s;i)),nil) |
| | | Thm* For any graph
 the_obj:GraphObject(the_graph). depthfirst(the_obj) the_obj:GraphObject(the_graph). depthfirst(the_obj)  Traversal Traversal |
|
| depthfirst-traversal | Def depthfirst-traversal(the_graph;s) ==  i:Vertices(the_graph), s1,s2:traversal(the_graph). ( i:Vertices(the_graph), s1,s2:traversal(the_graph). ( j:Vertices(the_graph). i-the_graph- > *j j:Vertices(the_graph). i-the_graph- > *j    non-trivial-loop(the_graph;j)) non-trivial-loop(the_graph;j))   s = (s1 @ [inl(i)] @ s2) s = (s1 @ [inl(i)] @ s2)  traversal(the_graph) traversal(the_graph)   ( ( j:Vertices(the_graph). j:Vertices(the_graph).  j = i j = i   i-the_graph- > *j i-the_graph- > *j   (inl(j) (inl(j)  s2)) s2)) |
|
| df-traversal | Def df-traversal(G;s) == ( i:Vertices(G), s1,s2:traversal(G). s = (s1 @ [inr(i)] @ s2) i:Vertices(G), s1,s2:traversal(G). s = (s1 @ [inr(i)] @ s2)  traversal(G) traversal(G)   ( ( j:Vertices(G). (inr(j) j:Vertices(G). (inr(j)  s2) s2)    (inl(j) (inl(j)  s2) s2)   j-G- > *i)) & ( j-G- > *i)) & ( i:Vertices(G), s1,s2:traversal(G). ( i:Vertices(G), s1,s2:traversal(G). ( j:Vertices(G). i-G- > *j j:Vertices(G). i-G- > *j    non-trivial-loop(G;j)) non-trivial-loop(G;j))   s = (s1 @ [inl(i)] @ s2) s = (s1 @ [inl(i)] @ s2)  traversal(G) traversal(G)   ( ( j:Vertices(G). i-G- > *j j:Vertices(G). i-G- > *j   (inr(j) (inr(j)  s2))) s2))) |
|
| graphobj | Def GraphObject(the_graph) == eq:Vertices(the_graph)  Vertices(the_graph) Vertices(the_graph)  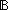  ( ( x,y:Vertices(the_graph). x,y:Vertices(the_graph). 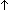 (eq(x,y)) (eq(x,y))   x = y) x = y) (eacc:( (eacc:(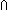 T:Type. (T T:Type. (T  Vertices(the_graph) Vertices(the_graph)  T) T)  T T  Vertices(the_graph) Vertices(the_graph)  T) T) ( ( T:Type, s:T, x:Vertices(the_graph), f:(T T:Type, s:T, x:Vertices(the_graph), f:(T  Vertices(the_graph) Vertices(the_graph)  T). T).  L:Vertices(the_graph) List. ( L:Vertices(the_graph) List. ( y:Vertices(the_graph). x-the_graph- > y y:Vertices(the_graph). x-the_graph- > y   (y (y  L)) & eacc(f,s,x) = list_accum(s',x'.f(s',x');s;L)) L)) & eacc(f,s,x) = list_accum(s',x'.f(s',x');s;L)) (vacc:( (vacc:(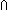 T:Type. (T T:Type. (T  Vertices(the_graph) Vertices(the_graph)  T) T)  T T  T) T) ( ( T:Type, s:T, f:(T T:Type, s:T, f:(T  Vertices(the_graph) Vertices(the_graph)  T). T).  L:Vertices(the_graph) List. no_repeats(Vertices(the_graph);L) & ( L:Vertices(the_graph) List. no_repeats(Vertices(the_graph);L) & ( y:Vertices(the_graph). (y y:Vertices(the_graph). (y  L)) & vacc(f,s) = list_accum(s',x'.f(s',x');s;L)) L)) & vacc(f,s) = list_accum(s',x'.f(s',x');s;L)) Top)) Top)) |
| | | Thm*  the_graph:Graph. GraphObject(the_graph) the_graph:Graph. GraphObject(the_graph)  Type{i'} Type{i'} |
|
| non-trivial-loop-free | Def non-trivial-loop-free(G) ==  i:Vertices(G). i:Vertices(G).  non-trivial-loop(G;i) non-trivial-loop(G;i) |
|
| topsorted | Def topsorted(the_graph;s) ==  i,j:Vertices(the_graph). i-the_graph- > *j i,j:Vertices(the_graph). i-the_graph- > *j    i = j i = j   i before j i before j  s s |
| | | Thm* For any graph
 s:V List. topsorted(the_graph;s) s:V List. topsorted(the_graph;s)  Prop Prop |
|
| gr_v | Def Vertices(t) == 1of(t) |
| | | Thm*  t:Graph. Vertices(t) t:Graph. Vertices(t)  Type Type |
|
| graph | Def Graph == v:Type e:Type e:Type (e (e  v v v) v) Top Top |
| | | Thm* Graph  Type{i'} Type{i'} |
|
| l_member | Def (x  l) == l) ==  i: i: . i < ||l|| & x = l[i] . i < ||l|| & x = l[i]  T T |
| | | Thm*  T:Type, x:T, l:T List. (x T:Type, x:T, l:T List. (x  l) l)  Prop Prop |
|
| no_repeats | Def no_repeats(T;l) ==  i,j: i,j: . i < ||l|| . i < ||l||   j < ||l|| j < ||l||    i = j i = j    l[i] = l[j] l[i] = l[j]  T T |
| | | Thm*  T:Type, l:T List. no_repeats(T;l) T:Type, l:T List. no_repeats(T;l)  Prop Prop |
|
| paren | Def paren(T;s) == s = nil  (T+T) List (T+T) List 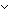 ( ( t:T, s':(T+T) List. s = ([inl(t)] @ s' @ [inr(t)]) & paren(T;s')) t:T, s':(T+T) List. s = ([inl(t)] @ s' @ [inr(t)]) & paren(T;s')) 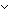 ( ( s',s'':(T+T) List. ||s'|| < ||s|| & ||s''|| < ||s|| & s = (s' @ s'') & paren(T;s') & paren(T;s'')) (recursive) s',s'':(T+T) List. ||s'|| < ||s|| & ||s''|| < ||s|| & s = (s' @ s'') & paren(T;s') & paren(T;s'')) (recursive) |
| | | Thm*  T:Type, s:(T+T) List. paren(T;s) T:Type, s:(T+T) List. paren(T;s)  Prop Prop |