| | Some definitions of interest. |
|
| adjm_adj | Def t.adj == 2of(t) |
| | | Thm*  t:AdjMatrix. t.adj t:AdjMatrix. t.adj   t.size t.size   t.size t.size  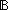 |
|
| adjm_size | Def t.size == 1of(t) |
| | | Thm*  t:AdjMatrix. t.size t:AdjMatrix. t.size   |
|
| adjmatrix | Def AdjMatrix == size:   size size   size size  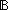 |
| | | Thm* AdjMatrix  Type Type |
|
| filter | Def filter(P;l) == reduce( a,v. if P(a) a,v. if P(a)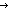 [a / v] else v fi;nil;l) [a / v] else v fi;nil;l) |
| | | Thm*  T:Type, P:(T T:Type, P:(T  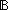 ), l:T List. filter(P;l) ), l:T List. filter(P;l)  T List T List |
|
| int_seg | Def {i..j } == {k: } == {k: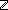 | i | i 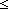 k < j } k < j } |
| | | Thm*  m,n: m,n: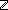 . {m..n . {m..n } }  Type Type |
|
| list_accum | Def list_accum(x,a.f(x;a);y;l) == Case of l; nil 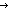 y ; b.l' y ; b.l' 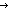 list_accum(x,a.f(x;a);f(y;b);l') (recursive) list_accum(x,a.f(x;a);f(y;b);l') (recursive) |
| | | Thm*  T,T':Type, l:T List, y:T', f:(T' T,T':Type, l:T List, y:T', f:(T'  T T  T'). list_accum(x,a.f(x,a);y;l) T'). list_accum(x,a.f(x,a);y;l)  T' T' |
|
| nat | Def  == {i: == {i: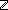 | 0 | 0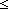 i } i } |
| | | Thm*   Type Type |
|
| primrec | Def primrec(n;b;c) == if n=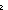 0 0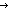 b else c(n-1,primrec(n-1;b;c)) fi (recursive) b else c(n-1,primrec(n-1;b;c)) fi (recursive) |
| | | Thm*  T:Type, n: T:Type, n: , b:T, c:( , b:T, c:( n n  T T  T). primrec(n;b;c) T). primrec(n;b;c)  T T |
|
| top | Def Top == Void given Void |
| | | Thm* Top  Type Type |
|
| upto | Def upto(i;j) == if i < 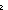 j j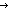 [i / upto(i+1;j)] else nil fi (recursive) [i / upto(i+1;j)] else nil fi (recursive) |
| | | Thm*  i,j: i,j: . upto(i;j) . upto(i;j)  {i..j {i..j } List } List |