| 1 | 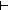 ||s1|| = ||s'|| ||s1|| = ||s'||  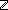 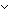 ||[inr(i) / s]|| = ||[inr(i) / s]|| ||[inr(i) / s]|| = ||[inr(i) / s]||  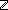 | 1 step |
| |
| 2 | 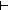 (s1 @ [inr(i) / s]) = (s' @ [inr(i) / s]) (s1 @ [inr(i) / s]) = (s' @ [inr(i) / s])  (Vertices(the_graph)+Vertices(the_graph)) List (Vertices(the_graph)+Vertices(the_graph)) List | 1 step |
| |
| 3 | 40. s1 = s'  (Vertices(the_graph)+Vertices(the_graph)) List (Vertices(the_graph)+Vertices(the_graph)) List
41. [inr(i) / s] = [inr(i) / s]  (Vertices(the_graph)+Vertices(the_graph)) List (Vertices(the_graph)+Vertices(the_graph)) List
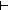 (inl(j) (inl(j)  s') s') | 1 step |