Thm*  'a:S. equal(nil,abs_list(pair(( 'a:S. equal(nil,abs_list(pair((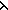 n:hnum. select( n:hnum. select(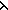 e:'a. t)),0))) e:'a. t)),0))) | [hnil_def] |
Thm*  'a:S. 'a:S.
Thm* and
Thm* (all(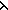 a:hlist('a). equal(abs_list(rep_list(a)),a)) a:hlist('a). equal(abs_list(rep_list(a)),a))
Thm* ,all
Thm* ,(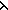 r:hprod((hnum r:hprod((hnum  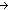 'a); hnum). equal 'a); hnum). equal
Thm* ,( r:hprod((hnum r:hprod((hnum   'a); hnum). (is_list_rep(r) 'a); hnum). (is_list_rep(r)
Thm* ,( r:hprod((hnum r:hprod((hnum   'a); hnum). ,equal(rep_list(abs_list(r)),r)))) 'a); hnum). ,equal(rep_list(abs_list(r)),r)))) | [hlist_iso_def] |
Thm*  'a:S. 'a:S.
Thm* exists
Thm* (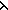 rep:hlist('a) rep:hlist('a)  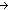 hprod((hnum hprod((hnum  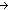 'a); hnum). type_definition 'a); hnum). type_definition
Thm* ( rep:hlist('a) rep:hlist('a)   hprod((hnum hprod((hnum   'a); hnum). (is_list_rep 'a); hnum). (is_list_rep
Thm* ( rep:hlist('a) rep:hlist('a)   hprod((hnum hprod((hnum   'a); hnum). ,rep)) 'a); hnum). ,rep)) | [hlist_ty_def] |
Thm*  'a:S. iso_pair('a List;( 'a:S. iso_pair('a List;(  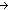 'a) 'a)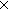  ;is_list_rep;rep_list;abs_list) ;is_list_rep;rep_list;abs_list) | [list_iso] |
Thm*  'a:S. 'a:S.
Thm* all
Thm* (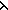 r:hprod((hnum r:hprod((hnum  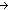 'a); hnum 'a); hnum
Thm* ( r:hprod(). equal r:hprod(). equal
Thm* ( r:hprod(). (is_list_rep(r) r:hprod(). (is_list_rep(r)
Thm* ( r:hprod(). ,exists r:hprod(). ,exists
Thm* ( r:hprod(). ,( r:hprod(). ,(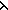 f:hnum f:hnum  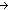 'a. exists 'a. exists
Thm* ( r:hprod(). ,( r:hprod(). ,( f:hnum f:hnum   'a. ( 'a. (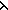 n:hnum. equal n:hnum. equal
Thm* ( r:hprod(). ,( r:hprod(). ,( f:hnum f:hnum   'a. ( 'a. ( n:hnum. (r n:hnum. (r
Thm* ( r:hprod(). ,( r:hprod(). ,( f:hnum f:hnum   'a. ( 'a. ( n:hnum. ,pair n:hnum. ,pair
Thm* ( r:hprod(). ,( r:hprod(). ,( f:hnum f:hnum   'a. ( 'a. ( n:hnum. ,(( n:hnum. ,((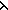 m:hnum. cond m:hnum. cond
Thm* ( r:hprod(). ,( r:hprod(). ,( f:hnum f:hnum   'a. ( 'a. ( n:hnum. ,(( n:hnum. ,(( m:hnum. (lt(m,n) m:hnum. (lt(m,n)
Thm* ( r:hprod(). ,( r:hprod(). ,( f:hnum f:hnum   'a. ( 'a. ( n:hnum. ,(( n:hnum. ,(( m:hnum. ,f(m) m:hnum. ,f(m)
Thm* ( r:hprod(). ,( r:hprod(). ,( f:hnum f:hnum   'a. ( 'a. ( n:hnum. ,(( n:hnum. ,(( m:hnum. ,select( m:hnum. ,select(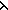 x:'a. t))) x:'a. t)))
Thm* ( r:hprod(). ,( r:hprod(). ,( f:hnum f:hnum   'a. ( 'a. ( n:hnum. ,,n)))))) n:hnum. ,,n)))))) | [his_list_rep_wd] |
Thm*  'a:S. hlist('a) 'a:S. hlist('a) 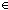 S S | [hlist_wf] |
Thm*  'a:S. el 'a:S. el 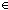 (hnum (hnum  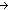 hlist('a) hlist('a)  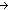 'a) 'a) | [hel_wf] |
Thm*  'a:S. hd 'a:S. hd 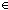 (hlist('a) (hlist('a)  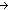 'a) 'a) | [hhd_wf] |
Thm*  'a:S, n: 'a:S, n: , l:'a List. n<||l|| , l:'a List. n<||l|| 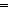 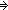 el(n,l) = l[n] el(n,l) = l[n] | [hel_nuprl] |
Thm*  'a:S, l:'a List. 'a:S, l:'a List. 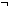 mt(l) mt(l) 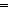 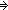 hd(l) = head(l) hd(l) = head(l) | [hhd_nuprl] |
Thm*  l:'a List. Dec(mt(l)) l:'a List. Dec(mt(l)) | [decidable__mt] |
Thm*  'a:S. 'a List 'a:S. 'a List 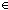 S S | [list_wf_stype] |
Thm*  'a:Type, p:('a 'a:Type, p:('a 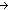 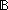 ), l:'a List. every(p;l) ), l:'a List. every(p;l) 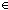 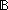 | [every_wf] |
Thm*  'a,'b,'c:Type, f:('a 'a,'b,'c:Type, f:('a 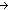 'b 'b 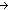 'c), l1:'a List, l2:'b List. 'c), l1:'a List, l2:'b List.
Thm* map2(f;l1;l2) 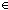 'c List 'c List | [map2_wf] |
Thm*  'a:Type, l:('a List) List. flatten(l) 'a:Type, l:('a List) List. flatten(l) 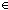 'a List 'a List | [flatten_wf] |
Thm* it_sum(nil) = 0
Thm* & ( l: l: List. List. 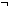 mt(l) mt(l) 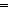 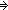 it_sum(l) = head(l)+it_sum(tl(l))) it_sum(l) = head(l)+it_sum(tl(l)))
Thm* & ( x: x: , l: , l: List. it_sum(cons(x; l)) = x+it_sum(l)) List. it_sum(cons(x; l)) = x+it_sum(l)) | [it_sum_def] |
Thm*  l: l: List. it_sum(l) List. it_sum(l) 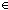  | [it_sum_wf] |
Thm*  'a:S, l:'a List. rep_list('a;l) 'a:S, l:'a List. rep_list('a;l) 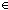 ( (  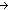 'a) 'a)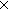  | [rep_list_wf] |
Thm* mt(nil) = True 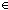 Prop{1} Prop{1}
Thm* & ( 'a:Type{i}, x:'a, l:'a List. mt(cons(x; l)) = False 'a:Type{i}, x:'a, l:'a List. mt(cons(x; l)) = False 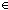 Prop{1}) Prop{1}) | [mt_def] |
Thm*  'a:Type, l:'a List. ||l|| 'a:Type, l:'a List. ||l|| 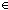  | [length_wf_nat] |
Thm*  l:'a List. null(l) l:'a List. null(l) 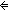 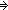 mt(l) mt(l) | [assert_of_null_is_mt] |
Thm*  'a:Type, l:'a List. 'a:Type, l:'a List. 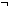 mt(l) mt(l) 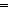 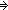 head(l) head(l) 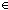 'a 'a | [head_wf] |
Thm*  l,ll:'a List. mt(l @ ll) l,ll:'a List. mt(l @ ll) 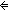 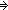 mt(l) & mt(ll) mt(l) & mt(ll) | [mt_append] |
Thm*  'a:Type{i}, l:'a List. mt(l) 'a:Type{i}, l:'a List. mt(l) 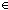 Prop{1} Prop{1} | [mt_wf] |