| 1 |
3. x' : hsum('a; 'b)
4. x'' : hsum('a; 'b)
5. rep_sum(x') = rep_sum(x'')  hbool hbool  'a 'a  'b 'b  hbool hbool
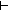 x' = x'' x' = x''
 | 1 step |
| 2 |
3. x : hbool  'a 'a  'b 'b  hbool hbool
4. ( f: f:   'a 'a  'b 'b   . . 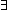 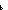 u:'a+'b. (f = u:'a+'b. (f =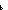 (rep_sum(u))))(x) (rep_sum(u))))(x)
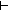 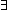 x':hsum('a; 'b). x = rep_sum(x') x':hsum('a; 'b). x = rep_sum(x')  hbool hbool  'a 'a  'b 'b  hbool hbool
 | 1 step |
| 3 |
3. x : hbool  'a 'a  'b 'b  hbool hbool
4. 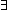 x':hsum('a; 'b). x = rep_sum(x') x':hsum('a; 'b). x = rep_sum(x')  hbool hbool  'a 'a  'b 'b  hbool hbool
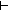 ( ( f: f:   'a 'a  'b 'b   . . 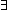 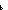 u:'a+'b. (f = u:'a+'b. (f =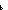 (rep_sum(u))))(x) (rep_sum(u))))(x)
 | 1 step |