| 1 |
1. f :    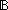
2. n : 
3. n 0 0
4. f(n)
5. f(0)
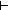 f(0) & ( f(0) & ( i: i: . i<0 . i<0   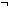 f(i)) f(i))
 | Auto |
| 2 |
1. f :    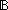
2. n : 
3. n 0 0
4. f(n)
5.  f(0) f(0)
 f(mu( f(mu( x.f(x+1))+1) & ( x.f(x+1))+1) & ( i: i: . i<mu( . i<mu( x.f(x+1))+1 x.f(x+1))+1   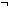 f(i)) f(i))
 | 1 step |
| 3 |
1. b : 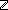
2. 0<b
3.  f:( f:(   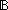 ). ( ). (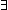 n: n: . n . n b-1 & f(n)) b-1 & f(n))   f(mu(f)) & ( f(mu(f)) & ( i: i: . i<mu(f) . i<mu(f)   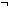 f(i)) f(i))
4. f :    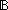
5. n : 
6. n b b
7. f(n)
8. f(0)
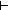 f(0) & ( f(0) & ( i: i: . i<0 . i<0   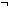 f(i)) f(i))
 | Auto |
| 4 |
1. b : 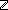
2. 0<b
3.  f:( f:(   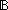 ). ( ). (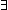 n: n: . n . n b-1 & f(n)) b-1 & f(n))   f(mu(f)) & ( f(mu(f)) & ( i: i: . i<mu(f) . i<mu(f)   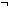 f(i)) f(i))
4. f :    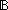
5. n : 
6. n b b
7. f(n)
8. 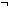 f(0) f(0)
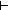 f(mu( f(mu(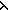 x.f(x+1))+1) & ( x.f(x+1))+1) & ( i: i: . i<mu( . i<mu(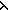 x.f(x+1))+1 x.f(x+1))+1   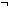 f(i)) f(i))
 | 11 steps |