| | Some definitions of interest. |
|
| d-realizes2 | Def D realizes2 es.P(es) ==  w:World, p:FairFifo. PossibleWorld(D;w) w:World, p:FairFifo. PossibleWorld(D;w)   P(ES(w)) P(ES(w)) |
|
| ma-da | Def M.da(a) == 1of(2of(M))(a)?Top |
|
| Kind-deq | Def KindDeq == union-deq(IdLnk Id;Id;product-deq(IdLnk;Id;IdLnkDeq;IdDeq);IdDeq) Id;Id;product-deq(IdLnk;Id;IdLnkDeq;IdDeq);IdDeq) |
|
| w-action | Def Action(i) == action(w-action-dec(w.TA;w.M;i)) |
|
| world | Def World
Def == T:Id  Id Id  Type Type
Def ==  TA:Id TA:Id  Id Id  Type Type
Def ==  M:IdLnk M:IdLnk  Id Id  Type Type
Def ==  (i:Id (i:Id     (x:Id (x:Id  T(i,x))) T(i,x))) (i:Id (i:Id     action(w-action-dec(TA;M;i))) action(w-action-dec(TA;M;i)))
Def == (i:Id     ({m:Msg(M)| source(mlnk(m)) = i } List)) ({m:Msg(M)| source(mlnk(m)) = i } List)) Top Top |
| | | Thm* World  Type{i'} Type{i'} |
|
| Knd | Def Knd == (IdLnk Id)+Id Id)+Id |
| | | Thm* Knd  Type Type |
|
| fair-fifo | Def FairFifo
Def == ( i:Id, t: i:Id, t: , l:IdLnk. , l:IdLnk.  source(l) = i source(l) = i   onlnk(l;m(i;t)) = nil onlnk(l;m(i;t)) = nil  Msg List) Msg List)
Def == & ( i:Id, t: i:Id, t: . .
Def == & ( isnull(a(i;t)) isnull(a(i;t))
Def == & ( 
Def == & (( x:Id. s(i;t+1).x = s(i;t).x x:Id. s(i;t+1).x = s(i;t).x  vartype(i;x)) vartype(i;x))
Def == & (& m(i;t) = nil  Msg List) Msg List)
Def == & ( i:Id, t: i:Id, t: , l:IdLnk. , l:IdLnk.
Def == & ( isrcv(l;a(i;t)) isrcv(l;a(i;t))
Def == & ( 
Def == & (destination(l) = i
Def == & (& ||queue(l;t)||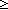 1 & hd(queue(l;t)) = msg(a(i;t)) 1 & hd(queue(l;t)) = msg(a(i;t))  Msg) Msg)
Def == & ( l:IdLnk, t: l:IdLnk, t: . .
Def == & ( t': t': . .
Def == & (t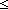 t' & t' &  isrcv(l;a(destination(l);t')) isrcv(l;a(destination(l);t'))  queue(l;t') = nil queue(l;t') = nil  Msg List) Msg List) |
|
| w-Msg | Def Msg == Msg(w.M) |
|
| IdLnk | Def IdLnk == Id Id Id  |
| | | Thm* IdLnk  Type Type |
|
| es-locl | Def (e <loc e') == loc(e) = loc(e')  Id & (e < e') Id & (e < e') |
|
| w-causl | Def e <c e' == e  e,e'. e <loc e' e,e'. e <loc e'   isrcv(kind(e')) & e = sender(e') isrcv(kind(e')) & e = sender(e')  E^+ e' E^+ e' |
|
| w-index | Def index(e)
Def == ||rcvs(lnk(kind(e));time(e))||-||snds(lnk(kind(e));time(sender(e)))|| |
|
| w-sender | Def sender(e) == <source(lnk(kind(e))),mu( t.match(lnk(kind(e));t;time(e)))> t.match(lnk(kind(e));t;time(e)))> |
|
| w-sends | Def sends(l;e) == onlnk(l;m(loc(e);time(e))) |
|
| w-onlnk | Def onlnk(l;mss) == filter( ms.mlnk(ms) = l;mss) ms.mlnk(ms) = l;mss) |
|
| w-withlnk | Def withlnk(l;mss) == mapfilter( ms.2of(ms); ms.2of(ms); ms.mlnk(ms) = l;mss) ms.mlnk(ms) = l;mss) |
|
| idlnk-deq | Def IdLnkDeq == product-deq(Id;Id  ;IdDeq;product-deq(Id; ;IdDeq;product-deq(Id; ;IdDeq;NatDeq)) ;IdDeq;NatDeq)) |
|
| ma-state | Def State(ds) == x:Id  ds(x)?Top ds(x)?Top |
|
| w-E | Def E == {p:(Id  )| )|   isnull(a(1of(p);2of(p))) } isnull(a(1of(p);2of(p))) } |
|
| Id | Def Id == Atom  |
| | | Thm* Id  Type Type |
|
| es-valtype | Def valtype(e) == if isrcv(e) rcvtype(e) else acttype(e) fi rcvtype(e) else acttype(e) fi |
|
| w-V | Def V(i;k) == kindcase(k;a.1of(2of(w))(i,a);l,tg.1of(2of(2of(w)))(l,tg)) |
|
| w-valtype | Def valtype(i;a) == kindcase(kind(a);a.w.TA(i,a);l,tg.w.M(l,tg)) |
|
| actof | Def act(k) == outr(k) |
| | | Thm*  k:Knd. islocal(k) k:Knd. islocal(k)   act(k) act(k)  Id Id |
|
| d-single-pre | Def @i (with ds: ds action a:T precondition a(v) is P s v)(j)
Def == if eqof(IdDeq)(j,i) (with ds: ds action a:T precondition a(v) is P s v) (with ds: ds action a:T precondition a(v) is P s v)
Def == else fi |
|
| deq | Def EqDecider(T) == eq:T  T T     x,y:T. x = y x,y:T. x = y 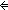   (eq(x,y)) (eq(x,y)) |
| | | Thm*  T:Type. EqDecider(T) T:Type. EqDecider(T)  Type Type |
|
| w-tagged | Def w-tagged(tg; mss) == filter( ms.mtag(ms) = tg;mss) ms.mtag(ms) = tg;mss) |
|
| eq_id | Def a = b == eqof(IdDeq)(a,b) |
| | | Thm*  a,b:Id. a = b a,b:Id. a = b   |
|
| fpf-val | Def z != f(x) ==> P(a;z) ==  x x  dom(f) dom(f)   P(x;f(x)) P(x;f(x)) |
|
| id-deq | Def IdDeq == product-deq(Atom; ;AtomDeq;NatDeq) ;AtomDeq;NatDeq) |
|
| product-deq | Def product-deq(A;B;a;b) == <proddeq(a;b),prod-deq(A;B;a;b)> |
|
| assert | Def  b == if b b == if b True else False fi True else False fi |
| | | Thm*  b: b: . b . b  Prop Prop |
|
| fpf-cap | Def f(x)?z == if x  dom(f) dom(f) f(x) else z fi f(x) else z fi |
|
| fpf-dom | Def x  dom(f) == deq-member(eq;x;1of(f)) dom(f) == deq-member(eq;x;1of(f)) |
|
| deq-member | Def deq-member(eq;x;L) == reduce( a,b. eqof(eq)(a,x) a,b. eqof(eq)(a,x)   b;false b;false ;L) ;L) |
|
| bor | Def p   q == if p q == if p true true else q fi else q fi |
| | | Thm*  p,q: p,q: . (p . (p   q) q)   |
|
| concat | Def concat(ll) == reduce( l,l'. l @ l';nil;ll) l,l'. l @ l';nil;ll) |
| | | Thm*  T:Type, ll:(T List) List. concat(ll) T:Type, ll:(T List) List. concat(ll)  T List T List |
|
| eqof | Def eqof(d) == 1of(d) |
| | | Thm*  T:Type, d:EqDecider(T). eqof(d) T:Type, d:EqDecider(T). eqof(d)  T T  T T   |
|
| es-E | Def E == 1of(es) |
|
| es-after | Def (x after e)
Def == 1of(2of(2of(2of(2of(2of(2of(2of(2of(2of(2of(es)))))))))))(x,e) |
|
| es-kind | Def kind(e) == 1of(2of(2of(2of(2of(2of(2of(2of(es))))))))(e) |
|
| es-loc | Def loc(e) == 1of(2of(2of(2of(2of(2of(2of(es)))))))(e) |
|
| es-val | Def val(e) == 1of(2of(2of(2of(2of(2of(2of(2of(2of(es)))))))))(e) |
|
| es-vartype | Def vartype(i;x) == 1of(2of(2of(es)))(i,x) |
|
| es-when | Def (x when e) == 1of(2of(2of(2of(2of(2of(2of(2of(2of(2of(es))))))))))(x,e) |
|
| fpf | Def a:A fp-> B(a) == d:A List a:{a:A| (a a:{a:A| (a  d) } d) }  B(a) B(a) |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type). a:A fp-> B(a) Type). a:A fp-> B(a)  Type Type |
|
| ma-empty | Def == mk-ma(; ; ; ; ; ; ; ) |
|
| fpf-empty | Def == <nil, x. x.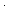 > > |
|
| islocal | Def islocal(k) ==   isl(k) isl(k) |
| | | Thm*  k:Knd. islocal(k) k:Knd. islocal(k)   |
|
| nat | Def  == {i: == {i: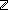 | 0 | 0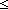 i } i } |
| | | Thm*   Type Type |
|
| le | Def A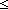 B == B ==  B<A B<A |
| | | Thm*  i,j: i,j: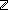 . (i . (i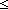 j) j)  Prop Prop |
|
| locl | Def locl(a) == inr(a) |
| | | Thm*  a:Id. locl(a) a:Id. locl(a)  Knd Knd |
|
| lsrc | Def source(l) == 1of(l) |
| | | Thm*  l:IdLnk. source(l) l:IdLnk. source(l)  Id Id |
|
| map | Def map(f;as) == Case of as; nil  nil ; a.as' nil ; a.as'  [(f(a)) / map(f;as')] [(f(a)) / map(f;as')]
Def (recursive) |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B), l:A List. map(f;l) B), l:A List. map(f;l)  B List B List |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B), l:A List B), l:A List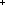 . map(f;l) . map(f;l)  B List B List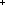 |
|
| nat-deq | Def NatDeq == < a,b. a= a,b. a= b,nat_DASH_deq_DASH_aux{1:l}> b,nat_DASH_deq_DASH_aux{1:l}> |
|
| not | Def  A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. ( A) A)  Prop Prop |
|
| w-M | Def w.M == 1of(2of(2of(w))) |
|
| w-ekind | Def kind(e) == kind(act(e)) |
|
| w-eval | Def val(e) == val(act(e)) |
|
| w-first | Def first(e)
Def == if time(e)= 0 0 true true
Def == i; isnull(a(loc(e);time(e)-1)) first(<loc(e),time(e)-1>) first(<loc(e),time(e)-1>)
Def == else false fi fi
Def (recursive) |
|
| w-pred | Def pred(e)
Def == if isnull(a(loc(e);time(e)-1)) pred(<loc(e),time(e)-1>) pred(<loc(e),time(e)-1>)
Def == else <loc(e),time(e)-1> fi
Def (recursive) |
|
| w-a | Def a(i;t) == 1of(2of(2of(2of(2of(w)))))(i,t) |
|
| w-after | Def (x after e) == s(1of(e);2of(e)+1).x |
|
| w-kind | Def kind(a) == 1of(outr(a)) |
|
| w-loc | Def loc(e) == 1of(e) |
|
| w-m | Def m(i;t) == 1of(2of(2of(2of(2of(2of(w))))))(i,t) |
|
| w-when | Def (x when e) == s(1of(e);2of(e)).x |
|
| w-s | Def s(i;t).x == 1of(2of(2of(2of(w))))(i,t,x) |
|
| w-vartype | Def vartype(i;x) == w.T(i,x) |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| w-val | Def val(a) == 2of(outr(a)) |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 2of(p) B(a)). 2of(p)  B(1of(p)) B(1of(p)) |
|
| rcv | Def rcv(l; tg) == inl(<l,tg>) |
| | | Thm*  l:IdLnk, tg:Id. rcv(l; tg) l:IdLnk, tg:Id. rcv(l; tg)  Knd Knd |
|
| top | Def Top == Void given Void |
| | | Thm* Top  Type Type |
|
| w-isnull | Def isnull(a) == isl(a) |