At: M DASH C DASH S SPACE induction 2 2 1 2 1 2 1 1 1
1. E: TaggedEventStruct
2. P: (|E| List)
Prop
3. I: (|E| List)Prop
4. memorylessR(E) preserves P
5. 
x,y,z:|E| List. P(x) 
P(y) (x
x.(yy.
(x =msg=(E) y))) & z = (x @ y) P(z)
6. x,y:|E| List. P(x) y 
x P(y)
7. safetyR(E) preserves I
8. tr:|E| List.
I(tr)
tr = nil
(
L_1,L_2:|E| List.
tr = (L_1 @ L_2)
& L_2 = nil
& (xL_1.(yL_2.(x =msg=(E) y)))
& (m:Label. (xL_2.tag(E)(x) = m)))
9. n: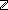 
10. 0 < n
11. tr:|E| List. ||tr||n-1 (m:Label. P( < tr > _m)) I(tr) P(tr)
12. tr: |E| List
13. ||tr||n
14. tr = nil
15. m:Label. P( < tr > _m)
16. I(tr)
17. L_1: |E| List
18. L_2: |E| List
19. tr = (L_1 @ L_2)
20. L_2 = nil
21. (xL_1.(yL_2.(x =msg=(E) y)))
22. m: Label
23. (xL_2.tag(E)(x) = m)
24. ||L_1||n-1
25. L_1 tr
26. I(L_1)
27. ||L_1||n-1
28. L_1 tr
29. I(L_1)
30. (m:Label. P( < L_1 > _m)) I(L_1) P(L_1)
31. m1: Label
32. P( < tr > _m1)
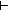< L_1 > _m1 < tr > _m1
By:
Unfold `tag_sublist` 0
THEN
BackThru
Thm* P:(T
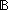), L2,L1:T List. L1 L2 filter(P;L1) filter(P;L2)
Generated subgoals:None
About:
