| 2 | 12.  i,j: i,j: ||tr||. i ||tr||. i j j   is-send(E)(tr[j]) is-send(E)(tr[j])   (i (switchR(tr)^*) ls) (i (switchR(tr)^*) ls)   (j (switchR(tr)^*) ls) (j (switchR(tr)^*) ls)
13. d: 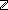
14. 0 < d
15.  i,j: i,j: ||tr||.
d-1 = j-i ||tr||.
d-1 = j-i   (i (switchR(tr)^*) ls)
(i (switchR(tr)^*) ls)   i i j j   ( ( k: k: ||tr||. (k (switchR(tr)^*) ls) & (tr[k] =msg=(E) tr[j])) ||tr||. (k (switchR(tr)^*) ls) & (tr[k] =msg=(E) tr[j]))
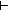  i,j: i,j: ||tr||.
d = j-i ||tr||.
d = j-i   (i (switchR(tr)^*) ls)
(i (switchR(tr)^*) ls)   i i j j   ( ( k: k: ||tr||. (k (switchR(tr)^*) ls) & (tr[k] =msg=(E) tr[j])) ||tr||. (k (switchR(tr)^*) ls) & (tr[k] =msg=(E) tr[j])) |