2. P : L:(T List)
(||L||-1)
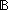
3. m : (T List)
4.
L:T List, i:(||L||-1).
4. P(L,i)
P(swap(L;i;i+1),i) & m(swap(L;i;i+1))<m(L)
5. L : T List
6. 0<||L||
7. f : (T List)
(T List)
8.
L:T List.
8. f(L)
8. =
8. if null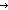(L)
L
8. else let i = search(||L||-1;P(L)) in if i=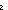
0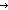 L else swap(L;i-1;i) fi fi
9.
x:T List. 
n:. f(f^n(x)) = f^n(x)
10. n :
11. f(f^n(L)) = f^n(L)
12. i :
(||f^n(L)||-1)
13. P(f^n(L),i)
14. (
i:(||f^n(L)||-1). P(f^n(L),i))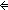 
(0<search(||f^n(L)||-1;P(f^n(L))))
15. 0<search(||f^n(L)||-1;P(f^n(L)))
16.
j:(||f^n(L)||-1). j<search(||f^n(L)||-1;P(f^n(L)))-1 P(f^n(L),j)
17.
n:, L:T List. ||f^n(L)|| = ||L||
18. j : {j':
| 0<j' & j'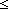
||f^n(L)|| }
19. search(||f^n(L)||-1;P(f^n(L))) = j
j-1+1<||f^n(L)||
