{ 
[A,B:Type]. [P,Q:dataflow(A;B)].
[ms:A List]. (data-stream(P;ms) = data-stream(Q;ms))
supposing a:A. as:A List. ((snd(P*(as)(a))) = (snd(Q*(as)(a)))) }
{ Proof }
Definitions occuring in Statement :
data-stream: data-stream(P;L),
iterate-dataflow: P*(inputs),
dataflow-ap: df(a),
dataflow: dataflow(A;B),
uimplies: b supposing a,
uall: [x:A]. B[x],
pi2: snd(t),
all: x:A. B[x],
list: type List,
universe: Type,
equal: s = t
Definitions :
union: left + right,
or: P 
Q,
assert: 
b,
divides: b | a,
assoced: a ~ b,
set_leq: a 
b,
set_lt: a <p b,
grp_lt: a < b,
cand: A c
B,
l_member: (x 
l),
l_contains: A 
B,
inject: Inj(A;B;f),
reducible: reducible(a),
prime: prime(a),
squash: 
T,
l_exists: (
xL. P[x]),
l_all: (xL.P[x]),
apply: f a,
infix_ap: x f y,
fun-connected: y is f*(x),
qle: r s,
qless: r < s,
q-rel: q-rel(r;x),
product: x:A 
B[x],
exists: x:A. B[x],
i-finite: i-finite(I),
i-closed: i-closed(I),
p-outcome: Outcome,
fset-member: a s,
f-subset: xs ys,
fset-closed: (s closed under fs),
l_disjoint: l_disjoint(T;l1;l2),
decidable: Dec(P),
void: Void,
top: Top,
set: {x:A| B[x]} ,
real: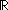 
,
grp_car: |g|,
subtype: S T,
int: 
,
nat: 
,
le: A B,
guard: {T},
implies: P 
Q,
lambda: 
x.A[x],
iterate-dataflow: P*(inputs),
dataflow-ap: df(a),
pi2: snd(t),
limited-type: LimitedType,
axiom: Ax,
data-stream: data-stream(P;L),
prop: 
,
member: t T,
uimplies: b supposing a,
uall: [x:A]. B[x],
so_lambda: 
x.t[x],
all: x:A. B[x],
function: x:A 
B[x],
equal: s = t,
list: type List,
dataflow: dataflow(A;B),
universe: Type,
isect: 
x:A. B[x],
ge: i 
j ,
false: False,
not: 
A,
minus: -n,
add: n + m,
subtract: n - m,
Auto: Error :Auto,
length: ||as||,
natural_number: $n,
less_than: a < b,
Decide: Error :Decide,
CollapseTHENA: Error :CollapseTHENA,
CollapseTHEN: Error :CollapseTHEN,
tactic: Error :tactic,
sqequal: s ~ t,
append: as @ bs,
firstn: firstn(n;as),
cons: [car / cdr],
last: last(L),
nil: [],
bool: 
,
pair: <a, b>,
corec: corec(T.F[T]),
primrec: primrec(n;b;c),
subtype_rel: A r B,
uiff: uiff(P;Q),
and: P Q,
hd: hd(l),
tl: tl(l),
strong-subtype: strong-subtype(A;B),
fpf: a:A fp-> B[a],
true: True,
int_iseg: {i...j},
rationals: 
,
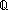RepUR: Error :RepUR,
RepeatFor: Error :RepeatFor,
lt_int: i <z j,
upto: upto(n),
iter_df_nil: iter_df_nil{iter_df_nil_compseq_tag_def:o}(P),
data_stream_nil: data_stream_nil{data_stream_nil_compseq_tag_def:o}(P)
Lemmas :
length_cons,
last_wf,
assert_wf,
pos_length2,
first0,
false_wf,
not_wf,
non_neg_length,
length_firstn,
true_wf,
squash_wf,
append_wf,
data-stream_wf,
firstn_wf,
data-stream-append,
firstn_all,
firstn_decomp,
ge_wf,
nat_properties,
nat_ind_tp,
guard_wf,
length_wf1,
le_wf,
comp_nat_ind_tp,
nat_wf,
uall_wf,
iterate-dataflow_wf,
dataflow-ap_wf,
pi2_wf,
dataflow_wf,
length_wf_nat,
top_wf,
member_wf,
decidable__lt
\mforall{}[A,B:Type]. \mforall{}[P,Q:dataflow(A;B)].
\mforall{}[ms:A List]. (data-stream(P;ms) = data-stream(Q;ms))
supposing \mforall{}a:A. \mforall{}as:A List. ((snd(P*(as)(a))) = (snd(Q*(as)(a))))
Date html generated:
2011_08_10-AM-08_16_41
Last ObjectModification:
2011_06_18-AM-08_31_05
Home
Index